Помогите пожалуйста))
Высота и радиус основания конуса равны.Найти радиус основания конуса,если его боковая поверхность равна 121 пи корень из 2.
Ответы
радиус основания конуса R=11
высота конуса h=R=11
образующая конуса L=11√2
Высота и радиус основания конуса равны.
Найти радиус основания конуса,если его боковая поверхность равна 121 пи корень из 2.
h=R
Sбок=121π√2
найти R - ?
площадь боковой поверхности конуса
Sбок=πRL, где L=√R²+h² образующая конуса
так как высота и радиус конуса равны h=R
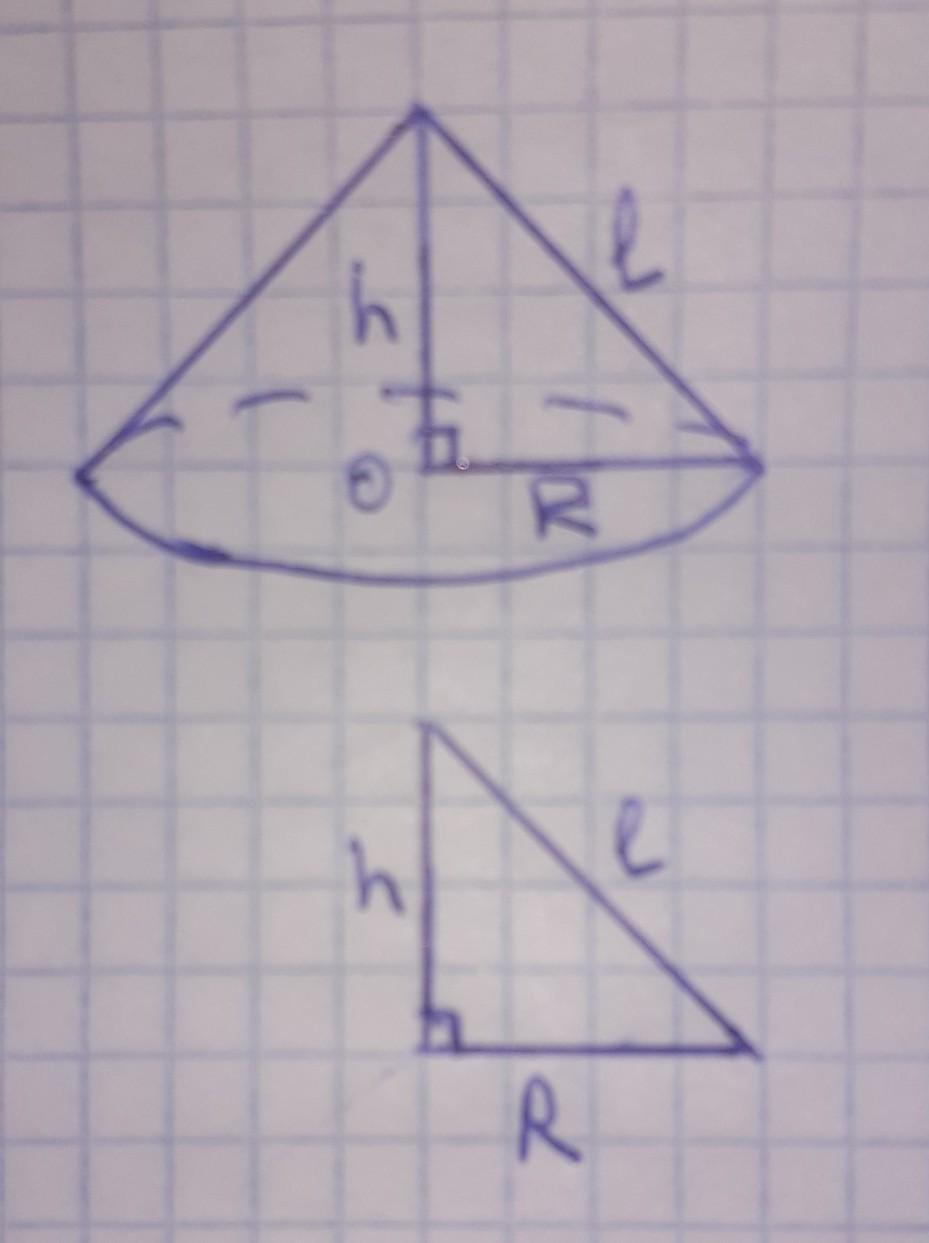
высота , радиус и образующая образует прямоугольный равнобедренный треугольник, где радиус и высота конуса катеты, а образующая конуса гипотенуза.
Заменим в формуле образующей конуса высоту на радиус тогда, длина образующей конуса будет L=√R²+R²=√2R²=R√2
это выходит от теоремы Пифагора.
В итоге формула площади боковой поверхности конуса будет выглядеть так
Sб=π×R×R×√2= π×R²×√2 , отсюда радиус
R=√Sб /(π√2)=√ (121π√2) / (π√2)=√121=11