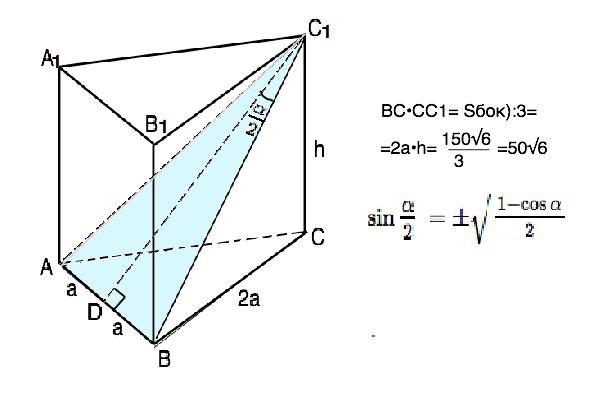
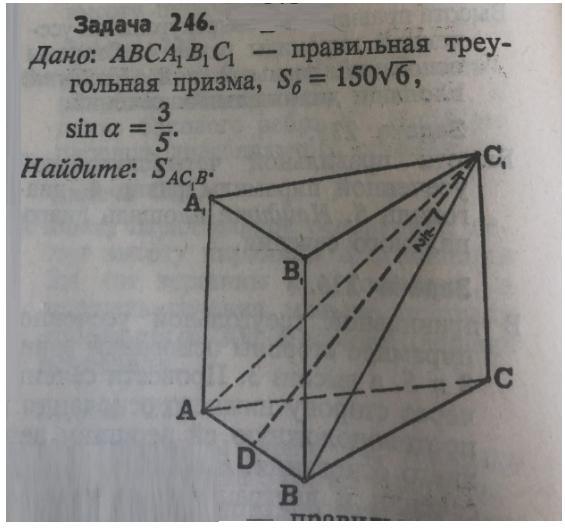
Дано: ABCA1B1C1 - правильная треугольная призма,
S(бок)=150√6,
sina=3/5.
Найти Ѕ(АС1В)
Ответы
Ответ: 75 (ед. площади)
Объяснение: Боковые рёбра правильной призмы перпендикулярны основанию, а в основании лежит правильный многоугольник, ⇒
∆ АВС - правильный.
По одной из формул площади треугольника Ѕ(АС1В)=0,5•АС1•ВС1•sinα
sinα=3/5 (дано).
Диагонали граней правильной призмы равны. ⇒ АС1=ВС1
На рисунке C1D делит угол пополам - С1D биссектриса ( медиана, высота) равнобедренного треугольника АС1В.
AD=BD
ВС1=BD/sin(BC1D)=BD/sin0,5α
Примем сторону основания равной 2а. Тогда BD=a.
По формуле половины угла sin0,5α=√((1-cosα)/2)
cosα=√(1-sin² α)=√(1-9/25)=4/5
sin0,5α=√((1-4/5):2)=√(1/10)=1/√10
BC1=a:1/√10 BC1=a√10
ВВ1С1С-прямоугольник. ВС1 - его диагональ.
Из ∆ ВСС1 по т.Пифагора СС1=√(BC1²-BC²)=√(10a²-4a²)=a√6
Из площади боковой поверхности площадь одной боковой грани BC•CC1=(150√6):3=50√6⇒
2a•a√6=50√6
2a²=50 ⇒ a=√(50/2)=5
АС1=ВС1=5√10
Ѕ(АС1В)=0,5•АС1•ВС1•sin(AC1B)=0,5•(5√10)²•3/5=0,5•250•3/5=75 (ед. площади)