Question

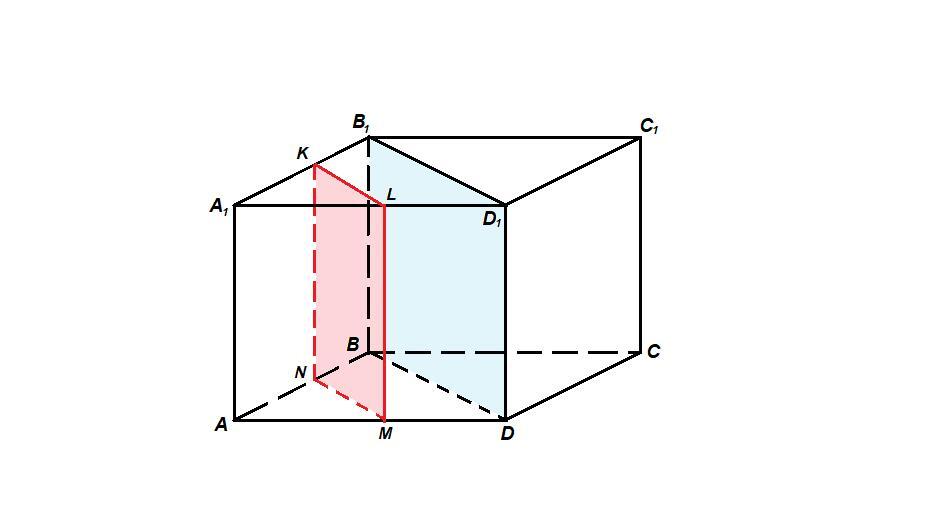
Постройте сечение параллелепипеда АВСДА1В1С1Д1 , проходящее через середину ребра АВ параллельно плоскости ВДД1

Answer 1

Ответ:

Плоскость BDD₁ пересекает грань ADD₁A₁ по прямой DD₁, значит она пересекает грань BCC₁B₁ по прямой ВВ₁, так как параллельные плоскости пересекаются третьей плоскостью по параллельным прямым.

BB₁D₁D - сечение параллелепипеда плоскостью BDD₁.

N - середина АВ.

Проведем MN - среднюю линию ΔABD, тогда MN║BD.

В грани ADD₁A₁ проведем ML║DD₁.

В грани ABB₁A₁ проведем NK║AA₁.

Соединим точки L  и  К.

KLMN - искомое сечение.

Доказательство:

Сечение проходит через точку N - середину ребра АВ.

NM║BD, ML║DD₁, значит плоскость (KLM) параллельна плоскости BDD₁ по признаку параллельности плоскостей (если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны)