Question

Очень срочно нужно ! Помогите пожалуйста
Взаимно перпендикулярные плоскости α и β пересекаются по прямой l .
В плоскости α отмечена точка А, в плоскости β – точка В. Прямая АВ
образует с плоскостью α угол, равный 30°. Найдите расстояние от точки В до
прямой l , если расстояние между точками А и В равно 17.

Answer 1

Ответ:

8,5

Пошаговое объяснение:

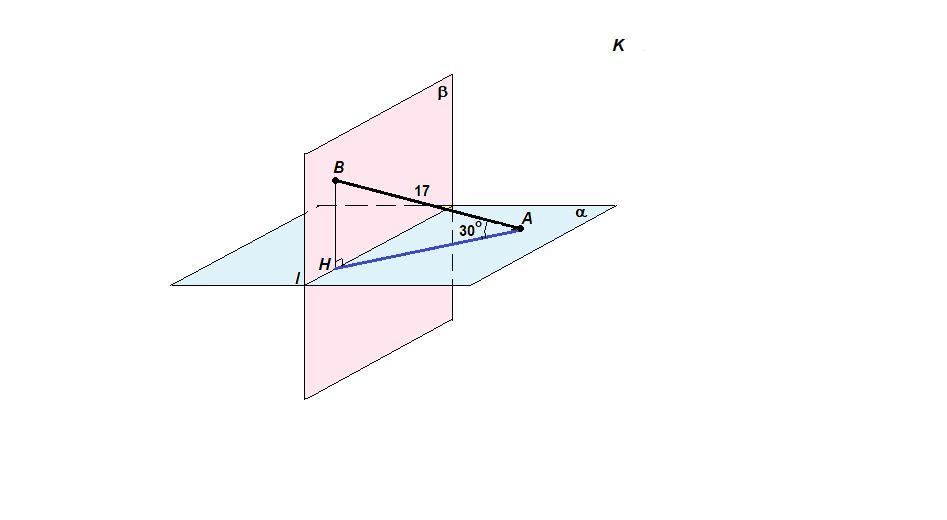
Проведем ВН⊥l, линии пересечения плоскостей.

ВН - искомое расстояние.

Если в одной из перпендикулярных плоскостей провести прямую, перпендикулярную к их линии пересечения, то прямая будет перпендикулярна другой плоскости.

Значит, ВН⊥α.

Тогда АН - проекция АВ на плоскость α.

Угол между прямой и плоскостью - это угол между прямой и ее проекцией на эту плоскость.

∠ВАН = 30°

ΔВАН:  ∠ВНА = 90°, ∠ВАН = 30°, значит ВН = АВ/2 = 17/2 = 8,5 по свойству катета, лежащего против угла в 30°.