Предмет: Математика,
автор: vrth90
Найти наибольшее значение функции y = 5x^2 - 20x - 1 на отрезке x подобно [1;3]
Ответы
Автор ответа:
0
y = 5x^2-20x-1, x ∈ [1;3]
max y - ?
Решение:
y' = 10x-20
y' = 0
10x-20 = 0
10x = 20
x = 2 — критическая точка
- y(2) = 5·2^2-20·2-1 = 20-40-1 = -21
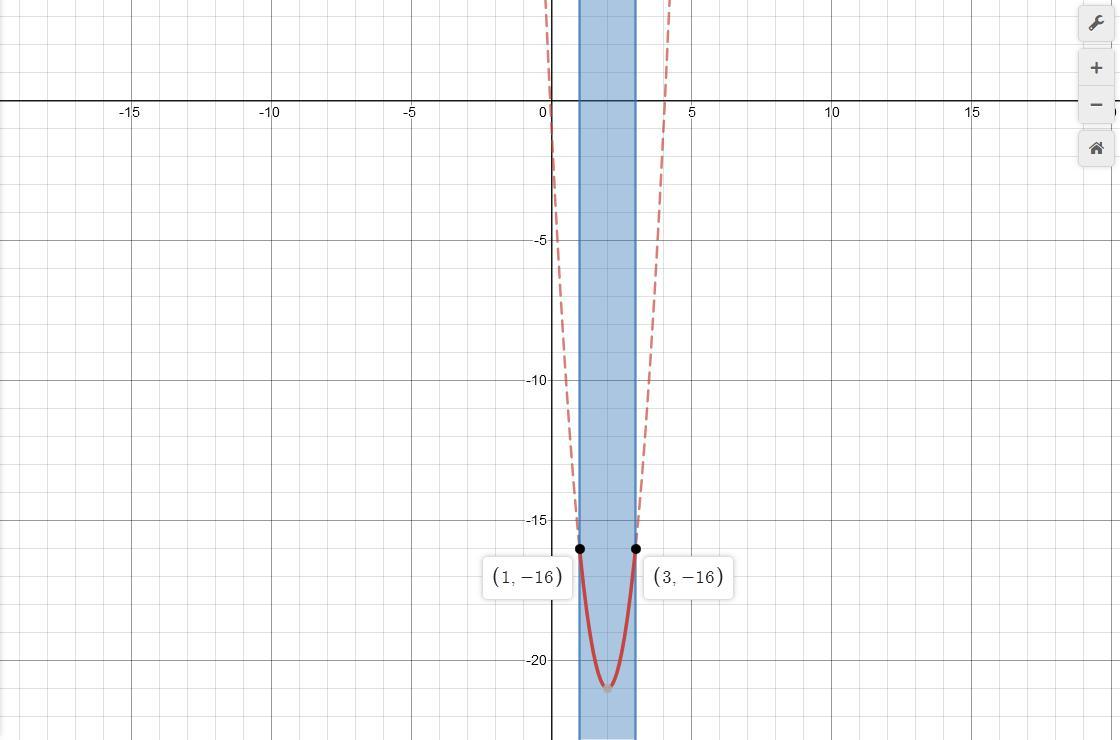
- y(1) = 5·1^2-20·1-1 = 5-20-1 = -16
- y(3) = 5·3^2-20·3-1 = 45-60-1 = -16
Ответ: max y(1) = -16 и max y(3) = -16; x ∈ [1;3].
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sofasim
Предмет: Русский язык,
автор: ivaskivivanna
Предмет: Русский язык,
автор: dianadi85
Предмет: Математика,
автор: vists
Предмет: Биология,
автор: Sukhanova2004