Предмет: Алгебра,
автор: 789456123579
Упростить выражения ( смотреть скриншот ниже )
Приложения:
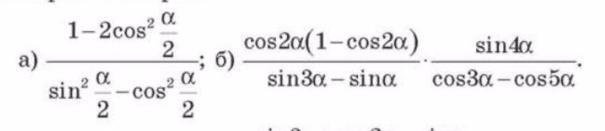
Ответы
Автор ответа:
1
a)
б)
Похожие вопросы
Предмет: Русский язык,
автор: ulayshka84
Предмет: Русский язык,
автор: ludvig9
Предмет: Русский язык,
автор: maisky03
Предмет: Литература,
автор: 5473894
Предмет: Химия,
автор: layaza4818