Question

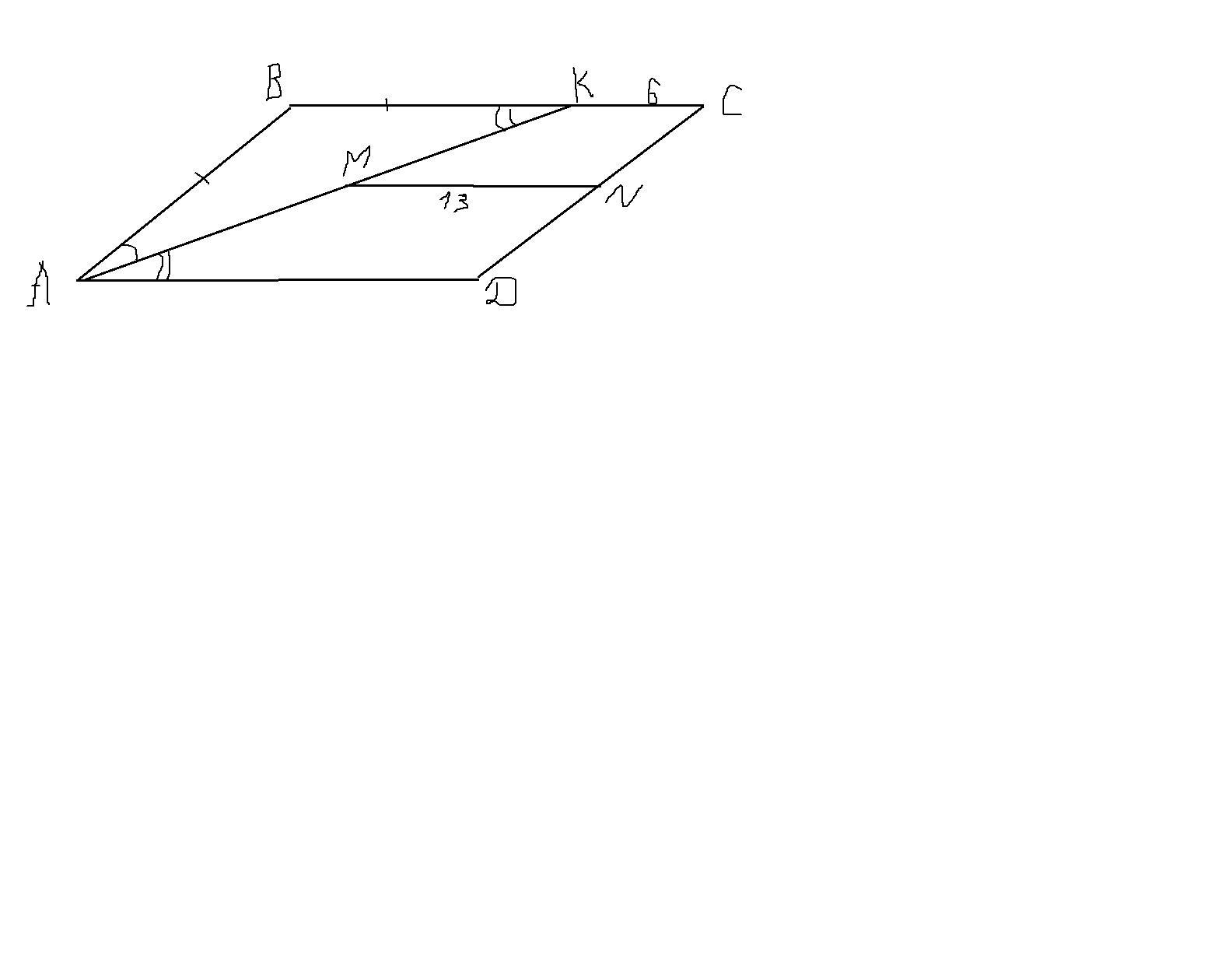
Дам 60 баллов!!!! Очень прошу помогите!!! В параллелограмме ABCD биссектриса угла А пересекает сторону BC в точке К. Найдите площадь параллелограмма(в см^2) если угол А=30 градусам,KC=6,а средняя линия трапеции AKCD равна 13 см.

Answer 1

Ответ:

S параллелограмма ABCD = 140 см^2

Пошаговое объяснение:

MN-средняя линия трапеции AKCD

MN=(KC+AD)/2

AD=2MN-KC

AD=2*13-6=20 см

AD=BC=20 см

BK=BC-KC=20-6=14 см

угол ВАК= углу КАD, так как АК- биссектриса

угол KAD= углу ВКА, так как ABCD-параллелограмм

AD║BC, AK-секущая

угол KAD= углу ВКА - накрест лежащие.

Тогда угол ВАК=углу ВКА, следовательно треугольник АВК - равнобедренный (углы при основании равны)

Получается , что АВ=ВК=14 см

угол А = 30 градусов (по условию)

S (ABCD) =AB*AD*sin30 градусов=14*20*1/2=140 см^2