помогите пж даю 40 балов

Ответы
Ответ:
Объяснение:
1) задание.
Сумма углов в треугольнике равна 180°
1)180°-40°=140° сумма двух углов при основании
В равнобедренном треугольнике углы при основании равны
2)140°:2=70° градусная мера угла при основании
Ответ: 70°
2) задание
На фото. Рис.2
3) задание
Угол <ОАЕ развернутый равен 180° рис. 1
Найдем угол <ВАЕ
<ВАЕ=<ОАЕ-<ОАВ
1)180°-100°=80° градусная мера угла ВАЕ
Пусть х будет градусная мера угла <ВЕА, тогда градусная мера угла <АВЕ равна х-30°, сумма углов в треугольнике равна 180°
Составляем уравнение
х+(х-30)+80=180
х+х-30=180-80
2х=100+30
2х=130
х=130:2
Х=65° градусная мера угла <ВЕА
Угол <АВЕ=х-30°
65°-30°=35° градусная мера угла <АВЕ
Ответ: <АВЕ=35°; <ВЕА=65°; <ВАЕ=80°
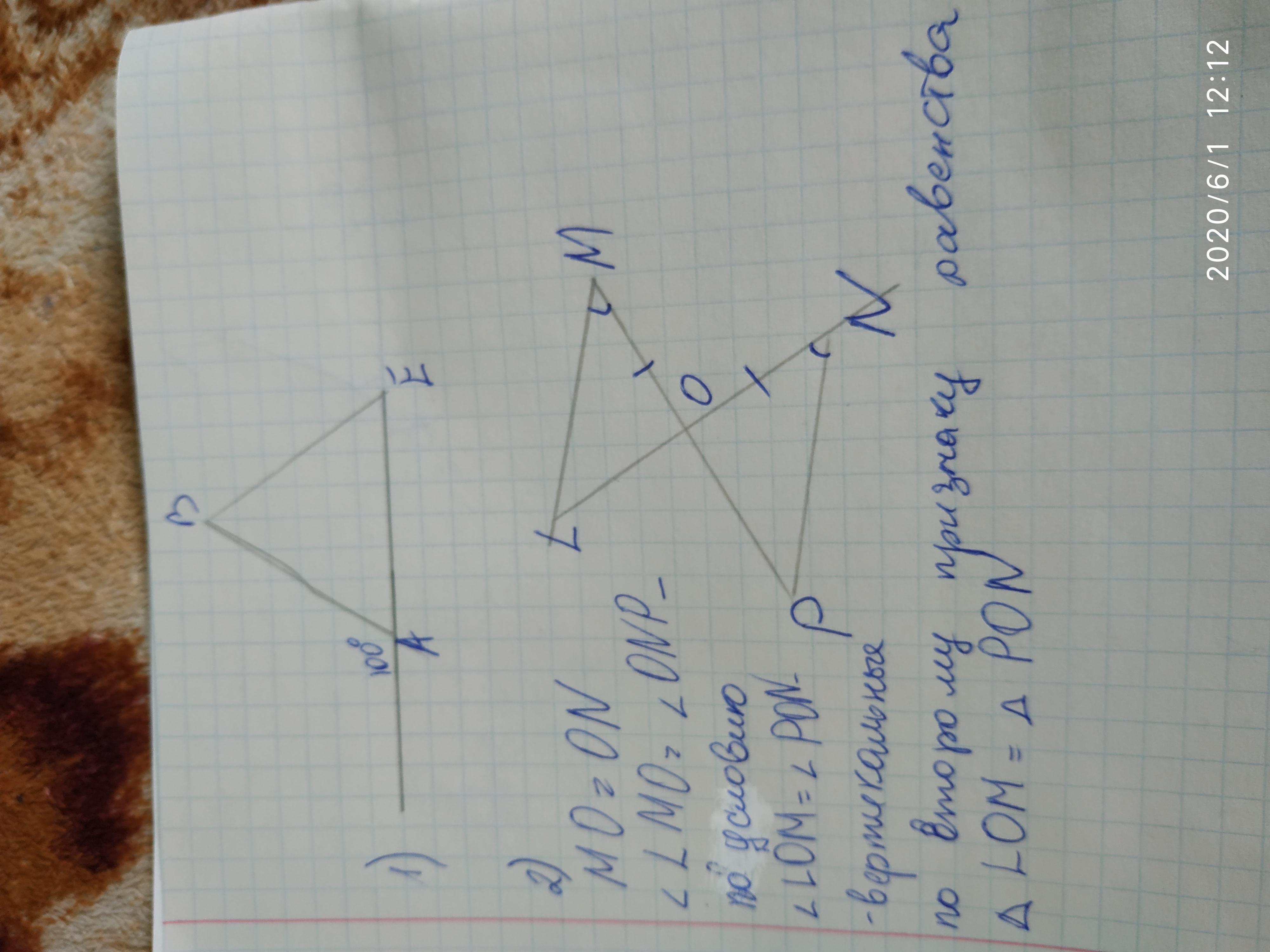
Задача#1.
Дано:
△АВС - равнобедренный.
∠В = 40°
Найти:
∠А, ∠С -?
Решение:
Так как △АВС - равнобедренный => ∠А = ∠С, по свойству равнобедренного треугольника.
Сумма углов треугольника равна 180°
180° - 40° = 140° - сумма ∠А и ∠С.
∠А = ∠С = 140°/2 = 70°
Ответ: 70°, 70°.
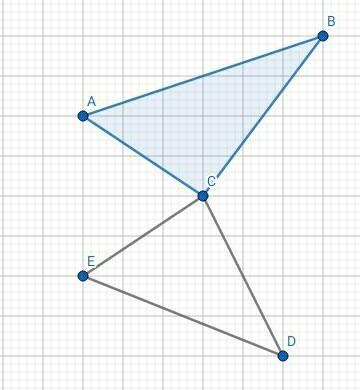
Задача#2.
Дано:
△АВС, △CED.
BC = CD
∠ABC = ∠CDE
Доказать:
△АВС = △CED
Решение:
Рассмотрим △АВС и △CED:
BC = CD, по условию.
∠АВС = ∠CDE, по условию.
Вертикальные углы равны.
∠АСВ = ∠ECD, как вертикальные.
=> △АВС = △CED, по 2 признаку равенства треугольников.
Ч.Т.Д.
Задача#3
Дано:
△АВЕ.
∠В - ? на 30° < ∠Е
∠А внешний = 100°
Найти:
∠В - ?
Решение:
Сумма смежных углов равна 180°.
∠А внутренний и ∠А внешний - смежные.
=> ∠А внутренний = 180˚ - 100˚ = 80˚
Пусть х° - ∠Е, х - 30° - ∠В, 80° - ∠А
Сумма углов треугольника равна 180°.
х + (х - 30) + 80 = 180
2х = 130
х = 65
65° - ∠Е
∠В = 65° - 30° = 35°
Ответ: 35°