Предмет: Геометрия,
автор: oshka3
у прямокутному трикутнику висота і медіана проведені з вершини прямого кута дорівнюють 24 і 26 знайти довжину бісектриси
Ответы
Автор ответа:
1
Ответ:
4,8√26 ед.
Объяснение:
В прямоугольном треугольнике АВС
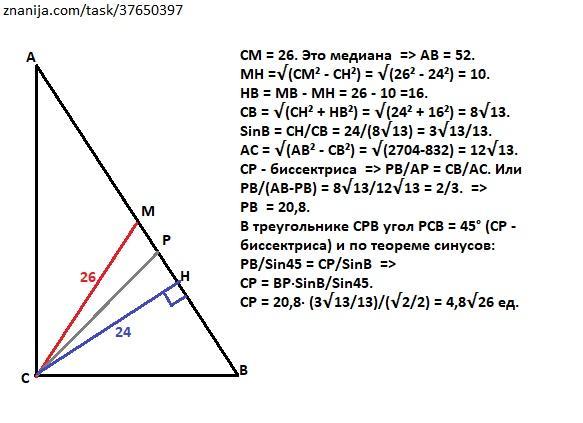
СМ = 26. Это медиана => АВ = 52.
В прямоугольном треугольнике ВСН по Пифагору:
МН =√(СМ² - СН²) = √(26² - 24²) = 10.
НВ = МВ - МН = 26 - 10 =16.
СВ = √(СН² + НВ²) = √(24² + 16²) = 8√13.
SinB = CH/CB = 24/(8√13) = 3√13/13.
АС = √(АВ² - СВ²) = √(2704-832) = 12√13.
СР - биссектриса => РВ/АР = СВ/АС. Или
РВ/(АВ-РВ) = 8√13/12√13 = 2/3. =>
РВ = 20,8.
В треугольнике СРВ угол РСВ = 45° (СР - биссектриса) и по теореме синусов: РВ/Sin45 = CP/SinB => CP = ВР·SinB/Sin45. =>
CP = 20,8· (3√13/13)/(√2/2) = 4,8√26 ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: vormex
Предмет: Русский язык,
автор: Lerailina99
Предмет: Английский язык,
автор: Рузали
Предмет: История,
автор: Аноним
Предмет: Литература,
автор: dias7980