Предмет: Математика,
автор: Krivchenkov02
Вычеслить интегралы (не использовать метод замены переменной) помогите плиз, даю 40 баллов
Приложения:
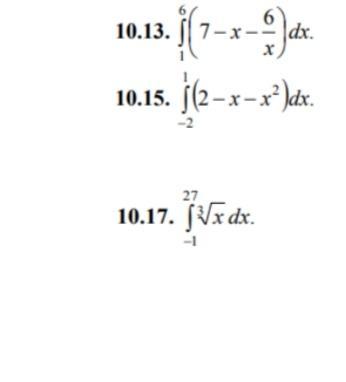
Ответы
Автор ответа:
1
Krivchenkov02:
Спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: ira83g
Предмет: Английский язык,
автор: mixaijlovaaa
Предмет: Русский язык,
автор: marinakalinina
Предмет: Химия,
автор: revogavriluk2
Предмет: Биология,
автор: OTRIX262