Предмет: Математика,
автор: yajatev651
ТРУБЫ ГОРЯТ РЕШИТЕ ПОЖАЛУЙСТА!!!
Приложения:
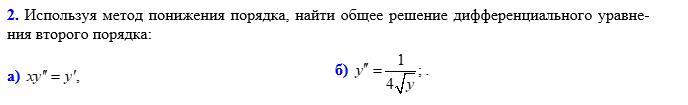
Ответы
Автор ответа:
0
a)
b)
Тут явно не выразить.
Похожие вопросы
Предмет: Русский язык,
автор: Sergey200111
Предмет: Английский язык,
автор: Крситинка777
Предмет: Қазақ тiлi,
автор: dashamatveykina
Предмет: Математика,
автор: dribotun