Предмет: Алгебра,
автор: dalanpavlov51
аж, помогите по алгебре
Приложения:
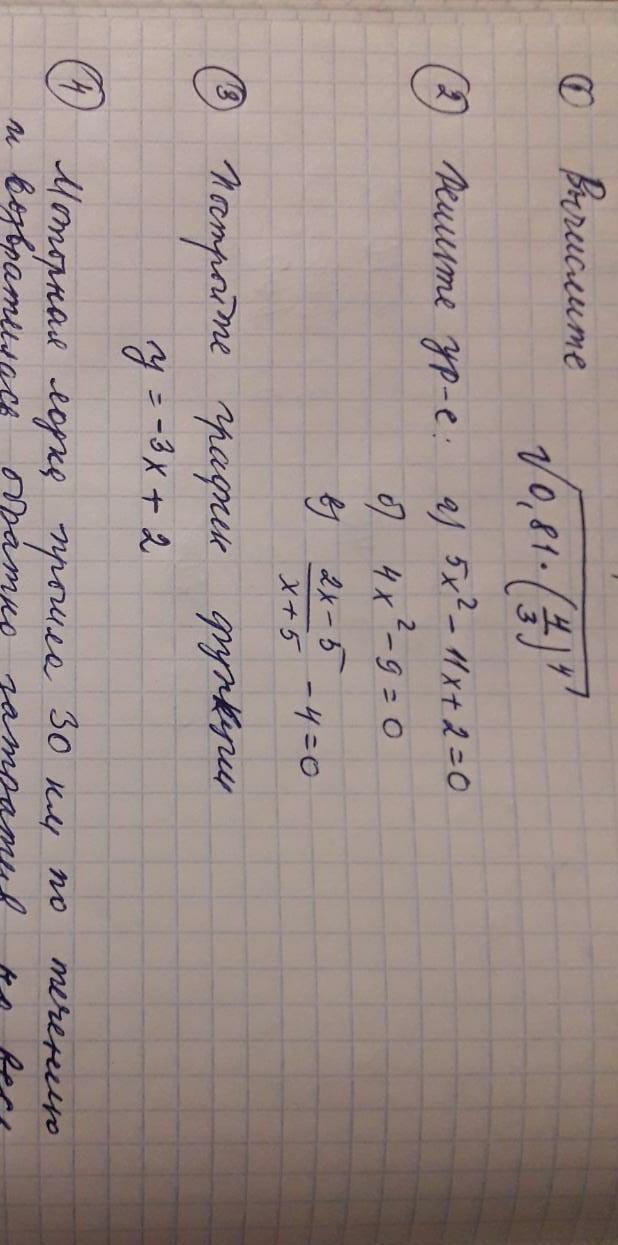
Alyssa08:
Вам нужно решить 3 задания?
да
Ответы
Автор ответа:
2
Задание #1.
Дано:
Найти:
Значение выражения.
Решение:
Ответ: 1,6
Задание #2.
Дано:
Найти:
Значения уравнений.
Решение:
----------------------
----------------------
Ответ: 1) x1=2, x2=0,2; 2) x1=1,5, x2=-1,5 3) x=-12,5.
Задание #3.
Дано:
Линейная функция .
Найти:
График данной линейной функции.
Решение:
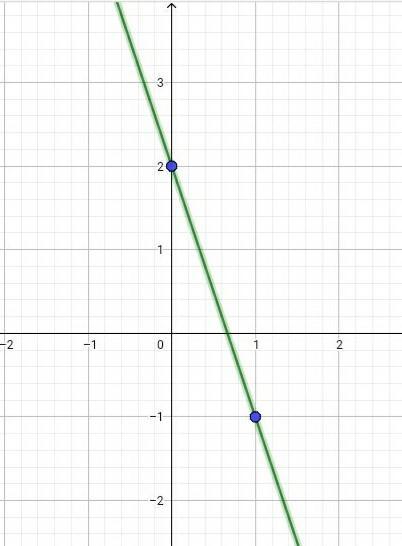
Дадим несколько значений аргументу, от чего будет зависеть значение линейной функции.
если x = 1, то у = -1;
если х = 0, то у = 2.
Ответ: график Вы сможете увидеть во вложении.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sanechka605
Предмет: Другие предметы,
автор: kviktorovna197
Предмет: Английский язык,
автор: pikalolesya
Предмет: Математика,
автор: DanilShumayev
Предмет: Алгебра,
автор: Kirill22800