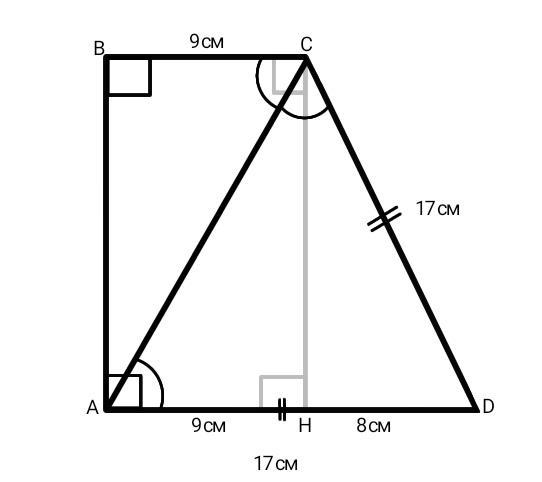
основания прямоугольной трапеции равны 9 и 17 см,а диагональ делит тупой угол пополам ,найти площадь трапеции
Ответы
Дано:
АВСD - прямоугольная трапеция.
ВС - меньшее основание = 9 см.
AD - большее основание = 17 см.
АС - диагональ, биссектриса тупого угла ВСD.
Найти:
S(ABCD) = ?
Решение:
Рассмотрим пару накрест лежащих углов BCA и АCD при параллельных прямых ВС и AD. Они равны, так как ВС||AD (по определению трапеции), следовательно, треугольник CAD - равнобедренный. Причём боковые стороны - это стороны AD и CD (так как они лежат против равных углов в одном треугольнике). AD = CD = 17 см.
Опустим из вершины тупого угла BCD на основание AD высоту CH. Рассмотрим четырёхугольник СНАВ. Все углы прямые, следовательно, четырёхугольник СНАВ - прямоугольник. У прямоугольника равны противоположные стороны, следовательно, ВС = АН = 9 см. Тогда НD = 17 см-9 см = 8 см.
Рассмотрим треугольник СНD - прямоугольный. По теореме Пифагора можем найти катет СН -
CD²-HD² = CH²
17²-8² = CH²
289-64 = CH²
CH² = 225
CH = √225
CH = 15 см.
Площадь трапеции равна произведению полусуммы оснований и высоты.
Высота - СН = 15 см.
Полусумма оснований - 0,5*(ВС+AD) = 0,5*(9 см+17 см) = 13 см.
S(ABCD) = 13 см*15 см = 195 см².
Ответ: 195 см².