Предмет: Математика,
автор: Аноним
помогите пожалуйста (18 и 19)
Приложения:
Ответы
Автор ответа:
1
Не люблю задания, в которых больше одной задачи. В следующий раз скорее всего буду их игнорировать.
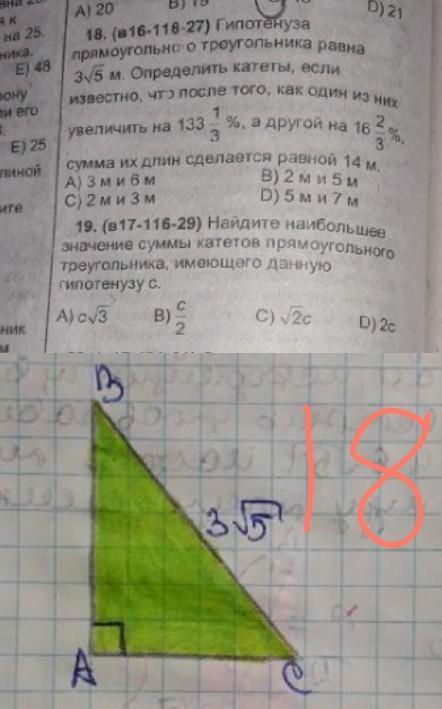
18) Катеты a и b, гипотенуза По условию
Поскольку по теореме Пифагора получаем
или
Годится только a=3, так как из условия 2a+b=12 следует, что 2a<12, a<6. А тогда b=12-6=6.
Ответ: A)
19)
Полученное выражение не может быть больше поскольку синус не бывает больше 1. Чтобы это выражение стало равно
синус должен быть равен 1, что означает, что
Ответ: C
Похожие вопросы
Предмет: Русский язык,
автор: liza101004
Предмет: Русский язык,
автор: катюша222
Предмет: Русский язык,
автор: artom49
Предмет: Обществознание,
автор: Сережа3214
Предмет: Физика,
автор: nata4656