Question

Заранее спасибо за помощь!!!!!

Answer 1

Ответ:

a = -3

Объяснение:

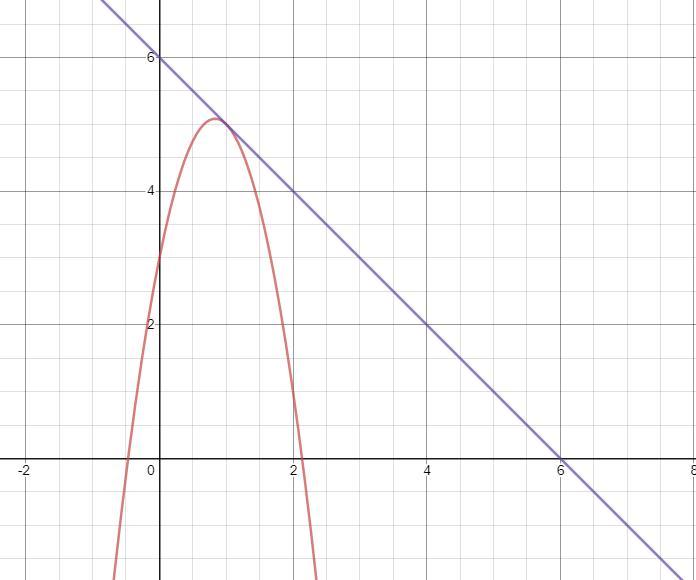
Пусть, f(x) = ax^2 + 5x + 3

Запишем уравнение касательной к графику в точке x0 = 1:

y = f(1) + f'(1)*(x-1).

Нужно найти f'(x).

f'(x) = 2ax + 5

Таким образом, уравнение касательной:

(a+8) + (2a + 5)*(x-1) = a+8+2ax+5x-2a-5 = x(2a+5) + (3-a)

Прямая составляет с осью x угол в 135 градусов, когда имеет вид

y = -x+p.

Значит, (2a+5) = -1

2a = -6

a = -3

---

Или же 2a+5 = 1, если нужен наклон в другую сторону (a = -2)