Question

Найдите интервалы возрастания и убывания функции f(x)= x^3-6x^2+9x-4. Желательно напишите на листе бумаги, все подробно и если нужно то и саму функцию

Answer 1

Ответ:

Объяснение:

Функция возрастает (убывает), когда ее производная положительна (отрицательна). Найдем f'(x):

f'(x) = 3x^2 - 12x + 9.

Найдем, в каких точках график производной пересекает ось абсцисс.

3x^2 - 12x + 9 = 0

x^2 - 4x + 3 = 0

(x-3)(x-1) = 0

x = 3 или x = 1.

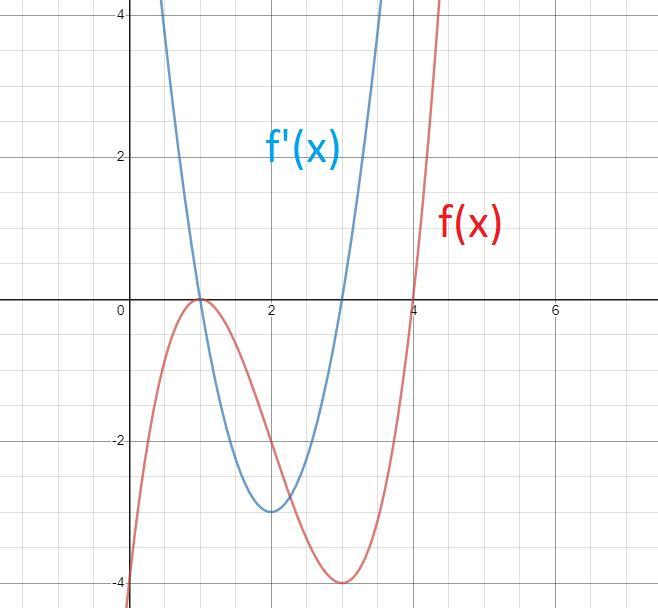
Получается, график производной - парабола с ветвями вверх, пересекающая ось абсцисс в точках 1 и 3.

Поэтому f(x) возрастает на x∈(-∞;1], затем убывает на x∈[1;3], и снова возрастает на x∈[3;+∞)