пожалуйста срочно!!

Ответы
Ответ: Решу пока первое задание
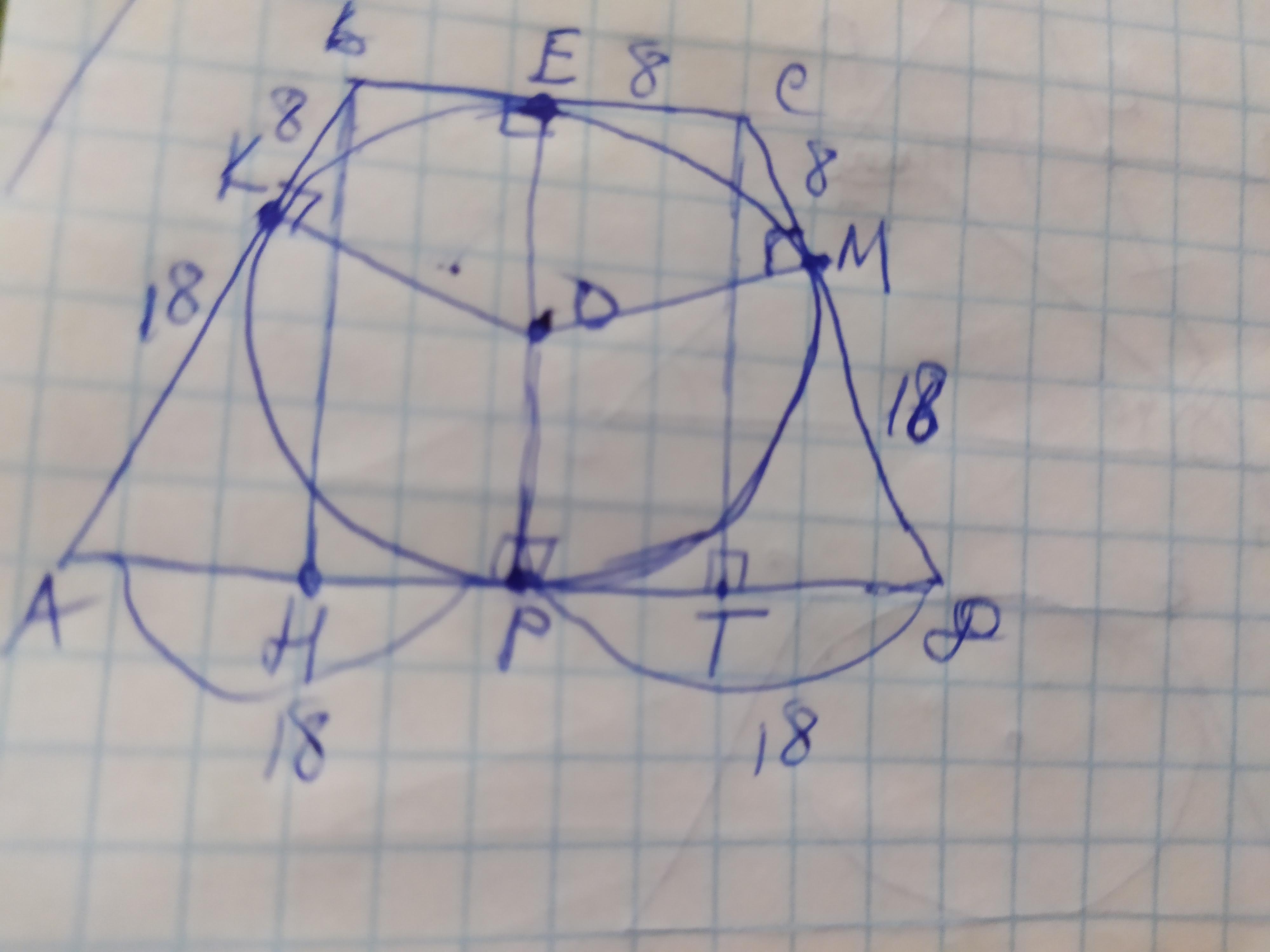
Объяснение: обозначим вершины трапеции А В С Д, а точки касания К Н М Р. Стороны трапеции являются касательными к вписанной окружности и соединяясь в одной вершине эти отрезки равны от вершины до точки касания. Поэтому:
ВК=ВК=ЕМ=8см; АК=АР=МД=РД=18см. Отсюда получим стороны трапеции:
АВ=СД=8+18=26см
ВС=8+8=16см
АД=18+18=36см. Проведём из вершин малого основания две высоты ВН и СТ. Они делят основание АД так, что НТ=ВС=16см. Так как трапеция равнобедренная то АН=ТД=(36-16)/2=
=20÷2=10см. Рассмотрим ∆АВН. Он прямоугольный и АВ в нём является гипотенузой, а ВН и АН– катеты. Найдём катет ВН по теореме Пифагора: ВН²=АВ²-АН²=26²-10²=
=676-100=576; ВН=√576=24
Мы нашли высоту трапеции, теперь найдём её площадь по формуле:
S= (ВС+АД)/2×ВН=
= (16+36)/2×24=52÷2×24=
=26×24=624см²
Ответ: S=624см²