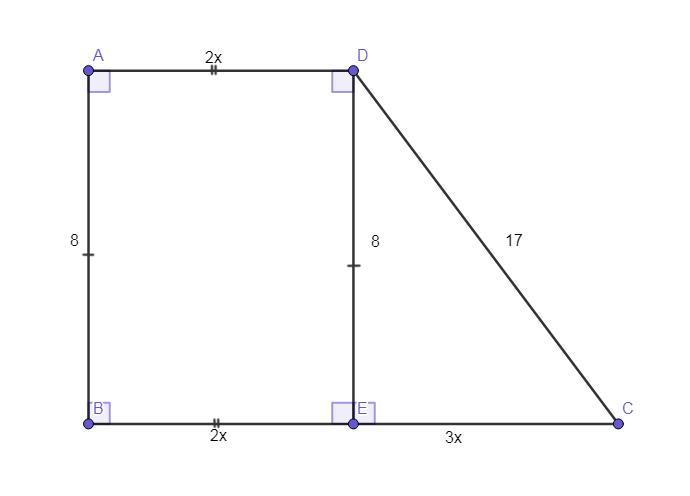
Боковые стороны прямоугольной трапеции равны 17 и 8, а её основание относятся как 2:5. Найдите площадь трапеции
Ответы
Проведём из вершины угла ∠ADC высоту DE на основание ВС трапеции ABCD. По свойству прямоугольной трапеции она равна меньшей боковой стороне АВ.
Пусть основание AD = 2х, тогда основание ВС = 5х.
Рассмотрим четырёхугольник ABED. У него все углы прямые, значит, четырёхугольник ABED - прямоугольник.
Противоположные стороны прямоугольника равны. АD = ВЕ = 2х. Следовательно, отрезок основания ЕС = 5х-2х = 3х.
Рассмотрим прямоугольный ΔDEC.
По теореме Пифагора -
DE²+EC² = DC²
EC² = DC²-DE²
Подставим в формулу известные нам значения -
(3х)² = 17²-8²
9х² = 289-64
9х² = 225
х² = 25
х₁ = -5 - не удовлетворяет условию.
х₂ = 5 - подходит.
Площадь трапеции равна полусумме её оснований и высоты.
Полусумма оснований = 0,5*(2х+5х) = 0,5*(2*5+5*5) = 0,5*(10+25) = 17,5.
Высота = 8.
Площадь трапеции = 17,5*8 = 140 (ед²).
Ответ: 140 (ед²).