Question

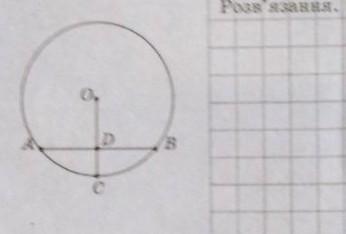
На рисунку радіус ОС коло проходить через середину хорди АВ.Знайдіть кут ОАВ , якщо кут ОСВ =60°​

Answer 1

Ответ: 30°.

Объяснение:

ΔОСВ: ОС=ОВ как радиусы одной окружности ⇒

ΔОСВ - равнобедренный, значит ∠ОВС=∠ОСВ=60° по свойству углов при основании равнобедренного треугольника.

Из теоремы о сумме углов треугольника:

∠СОВ=180°-(∠ОВС+∠ОСВ)=180°-(60°+60°)=60°.

ΔАОВ: АО=ВО как радиусы одной окружности ⇒

ΔАОВ - равнобедренный.

ОD- медиана ΔАОВ, т.к. АD=DВ по условию ⇒  ОD - биссектриса ⇒

∠ АОD=∠ВОD=60°,  ∠ АОВ=∠АОD+∠ВОD=60°+60°=120°.

∠ ОАВ=∠ ОВА по свойству углов при основании равнобедренного треугольника.

Из теоремы о сумме углов треугольника:

∠ ОАВ=(180°-120°):2=60°:2=30°.