Помогите пожалуйста!!! Срочно.
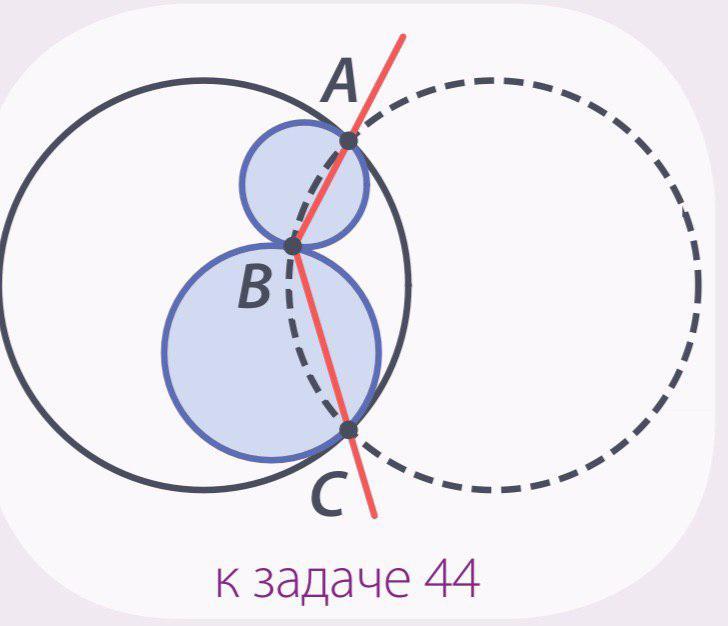
Две окружности внешним образом каса ются в точке В, а в точках А и С касаются третьей окружности изнутри. Оказалось, что радиус третьей окружности равен ради усу окружности, проходящей через точки А, В и С. Найдите угол АВС.
Ответы
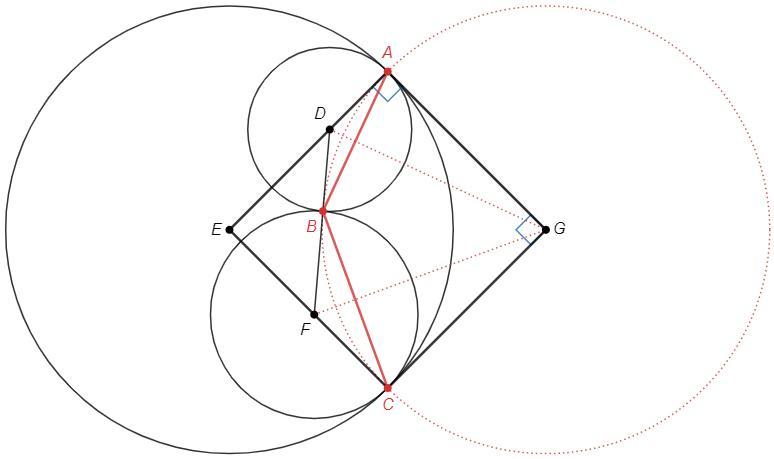
Центр G описанной окружности △ABC лежит на пересечении серединных перпендикуляров к сторонам AB и BC. Серединный перпендикуляр к хорде является биссектрисой центрального угла. DG - биссектриса ADB, FG - биссектриса BFC. Точка G является пересечением биссектрис внешних углов △DEF и центром вневписанной окружности.
EA=EC, DA=DB, FC=FB (радиусы)
ED+DA=EF+FC => ED+DB=EF+FB
Точка B делит периметр △DEF пополам, следовательно является точкой касания вневписанной окружности.
GB - радиус вневписанной окружности △DEF, следовательно GA также радиус этой окружности, A - точка касания. Радиус в точку касания перпендикулярен касательной, A=90.
EAGC - ромб (стороны равны как радиусы равных окружностей) с прямым углом A, следовательно квадрат, G=90.
∪AC=90, ∪CA=360-90=270, ABC=270/2=135