Предмет: Математика,
автор: 777alisham
Найти общее решение однородного дифференциального уравнения первого порядка
Приложения:
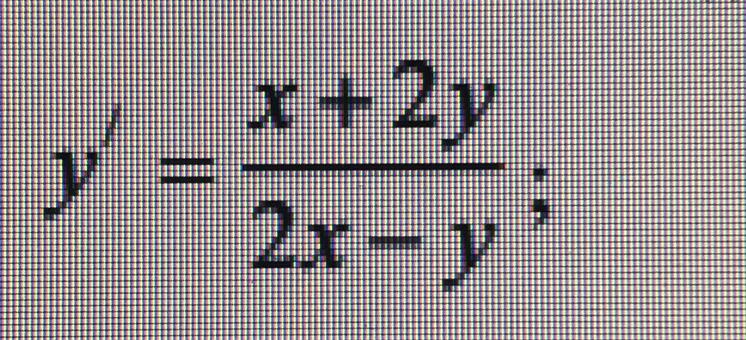
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: veronikam200
Предмет: Русский язык,
автор: 5Dominik5
Предмет: Русский язык,
автор: boris5000
Предмет: Физика,
автор: sfi201
Предмет: Литература,
автор: Жека4563