Предмет: Алгебра,
автор: botovich2017
Реши систему уравнений:
Приложения:
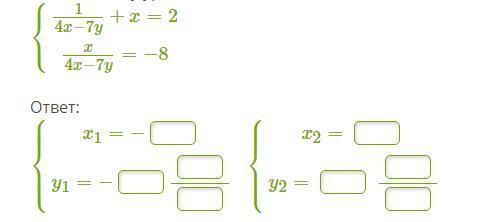
Ответы
Автор ответа:
1
Объяснение:
botovich2017:
Спасибо! Всё правильно)
Похожие вопросы
Предмет: Українська мова,
автор: Вова199999
Предмет: Русский язык,
автор: Sveta6347
Предмет: Українська мова,
автор: Вова199999
Предмет: Математика,
автор: галина235
Предмет: Химия,
автор: Кристя4728