Предмет: Алгебра,
автор: dariacerska
У кого есть сердце ♥, помогите!
Приложения:
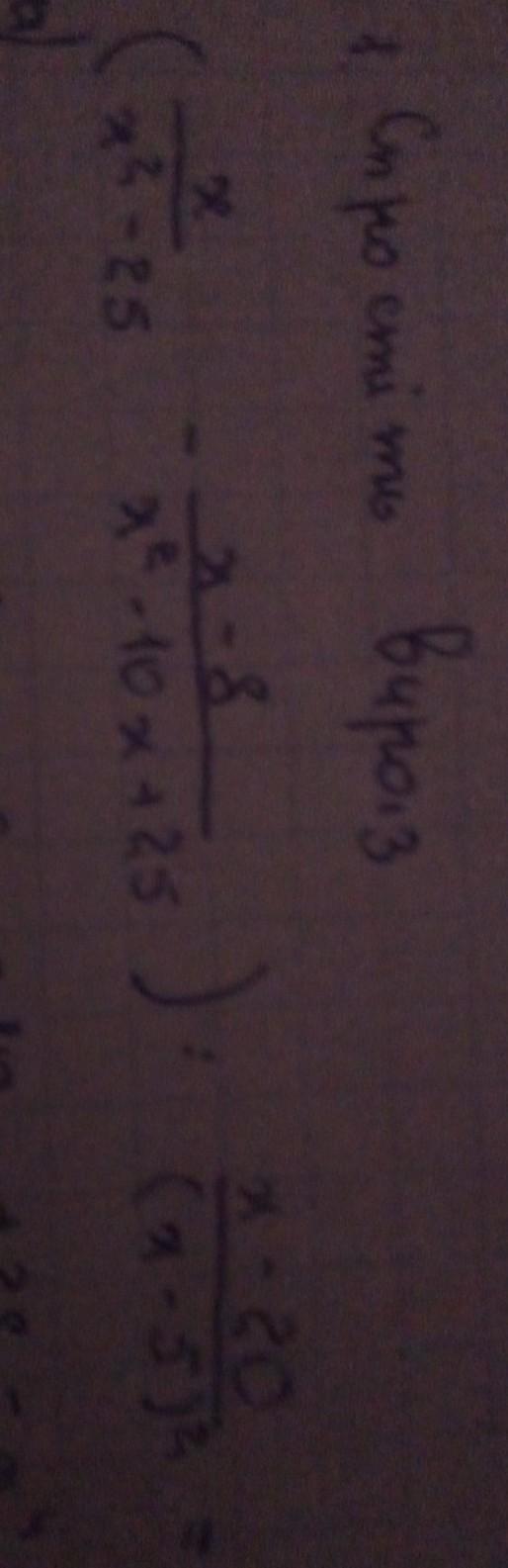
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: ЕленV
Предмет: Українська мова,
автор: DennaT
Предмет: Русский язык,
автор: nyurochek
Предмет: Музыка,
автор: Miss2017Karina