Предмет: Математика,
автор: Elizabeth5002
Даю много баллов!!
Две студенческие бригады могут выполнить задание, работая вместе 6ч. За сколько часов может выполнить это задание каждая бригада, работая самостоятельно, если одной из них для выполнения 2/5 задания нужна на 4 часа больше, чем другой для выполнения 1/5 задания.
Ответы
Автор ответа:
3
Ответ:
Если всю работу взять за 1.
Пусть первая бригада выполнит 1/5 задания за х часов
тогда вторая бригада за х+4 часа
Производительность труда при работе вместе бригад равна 1/6
Производительность первой бригады будет
производительность второй бригады
Исходя из этого получаем уравнение
Пошаговое объяснение:
Приложения:
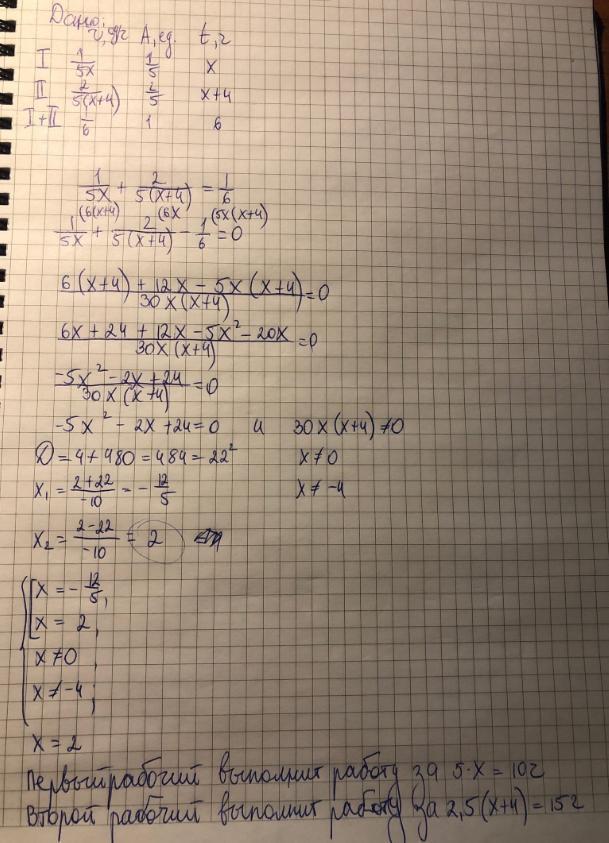
Похожие вопросы
Предмет: Русский язык,
автор: Chicago2
Предмет: Русский язык,
автор: 040305kt
Предмет: Русский язык,
автор: АнастасияОколович
Предмет: Алгебра,
автор: ПолинаКим13
Предмет: История,
автор: danilzharkov2