Предмет: Геометрия,
автор: Аноним
помогите пожалуйста решить с ДАНО это геометрия
Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке E. Найдите площадь параллелограмма ABCD если BE=7, EC=3, а угол ABC=150
Ответы
Автор ответа:
1
Дано:
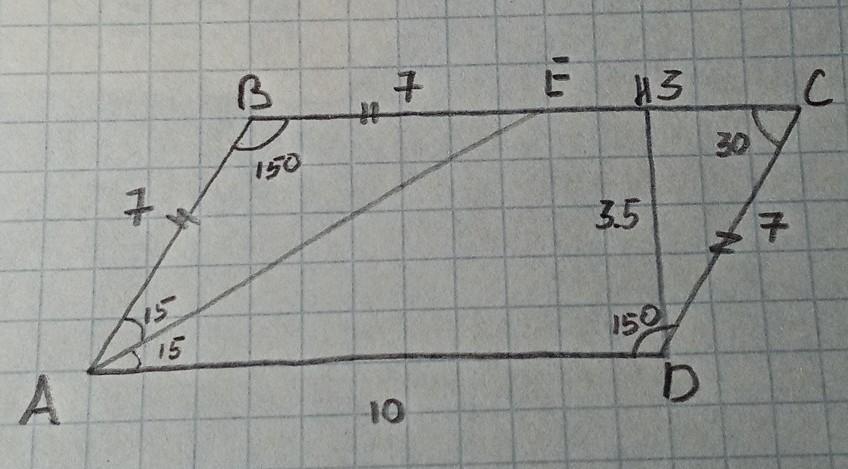
ABCD - параллелограмм, AE - биссектриса угла А, BE = 7, EC = 3, угол АВС =150°
Решение:
1) Так как ABCD - параллелограмм, следовательно, угол ABC = углу CDA, следовательно, уголы C и A = 30°
2) Так как ABCD - параллелограмм, а AE - биссектриса, следовательно, треугольник ABE - равнобедренный со сторонами 7, следовательно, BE=AB=DC=7
Проведем высоту DH
3) Треугольник CHD - прямоугольный с углом C=30°, следовательно, DH=1/2DC=3.5
4) BC=BE+EC=7+3=10
5) S параллелограмма = DH*BC=3.5*10=35
Ответ: 35
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sheshickova
Предмет: Русский язык,
автор: fdff
Предмет: Английский язык,
автор: murad553
Предмет: Математика,
автор: iraarje22
Предмет: Литература,
автор: лера1738