Предмет: Геометрия,
автор: rrrp6138
Биссектрисы углов А и B треугольника ABC пересекаются в точке м.
Найдите C, если АMB = 177
Alyssa08:
Здравствуйте, а не сказано, что треугольник АВС - равнобедренный или равносторонний?
нет
Ответы
Автор ответа:
4
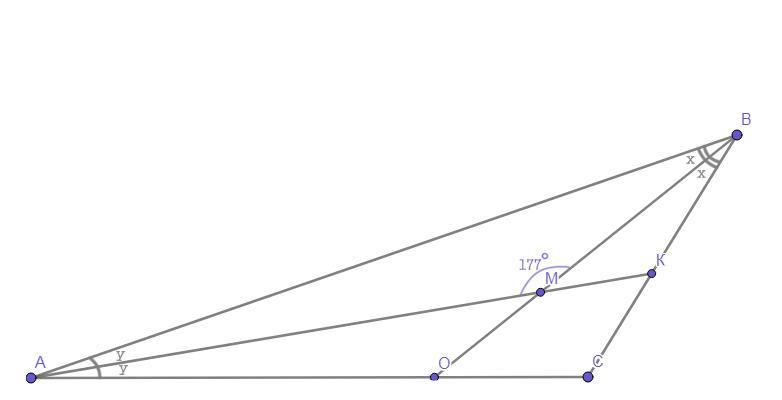
Чертёж смотрите во вложении.
Дано:
ΔАВС.
ВО - биссектриса ∠АВС.
АК - биссектриса ∠ВАС.
Точка М - точка пересечения ВО и АК.
∠АМВ = 177°.
Найти:
∠ВСА = ?
Решение:
Пусть ∠АВМ = х, тогда и ∠МВК = х (так как ВО - биссектриса ∠АВС) ; ∠ВАМ = ∠МАО = у (так как АК - биссектриса ∠ВАС).
Рассмотрим ΔАМВ. ∠ВМК - внешний, и так как он с ∠АМВ смежный, то ∠ВМК = 180°-177° = 3°. Так как ∠ВМК - внешний, то он равен сумме углов не смежных с ним. То есть, х+y = 3°.
∠АВС = x+x = 2x
∠ВАС = у+у = 2у.
х+у = 3°
2*(х+у) = 2*3°
2х+2у = 6°.
Тогда, по теореме о сумме углов треугольника -
∠ВСА = 180°-(2х+2у)
∠ВСА = 180°-6°
∠ВСА = 174°.
Ответ: 174°.
Приложения:
Привет, знаешь, лучше бы ты начертила угол С тупыми, так как он равен по твоему 174°.А то получается какая-то нестыковка.
тупым*
И что? Главное, что именно у меня в теоретической части всё верно. Но так уж и быть, сделаю его тупым :)
;-)
Похожие вопросы
Предмет: Английский язык,
автор: vbienrf15
Предмет: Русский язык,
автор: Nst95
Предмет: Английский язык,
автор: 00Julia00
Предмет: Физика,
автор: koroleva50201