Предмет: Алгебра,
автор: stasya1815
Найдите наибольшее и наименьшее значения функции: у=х+16/х на отрезке [1/2; 8]
Приложения:
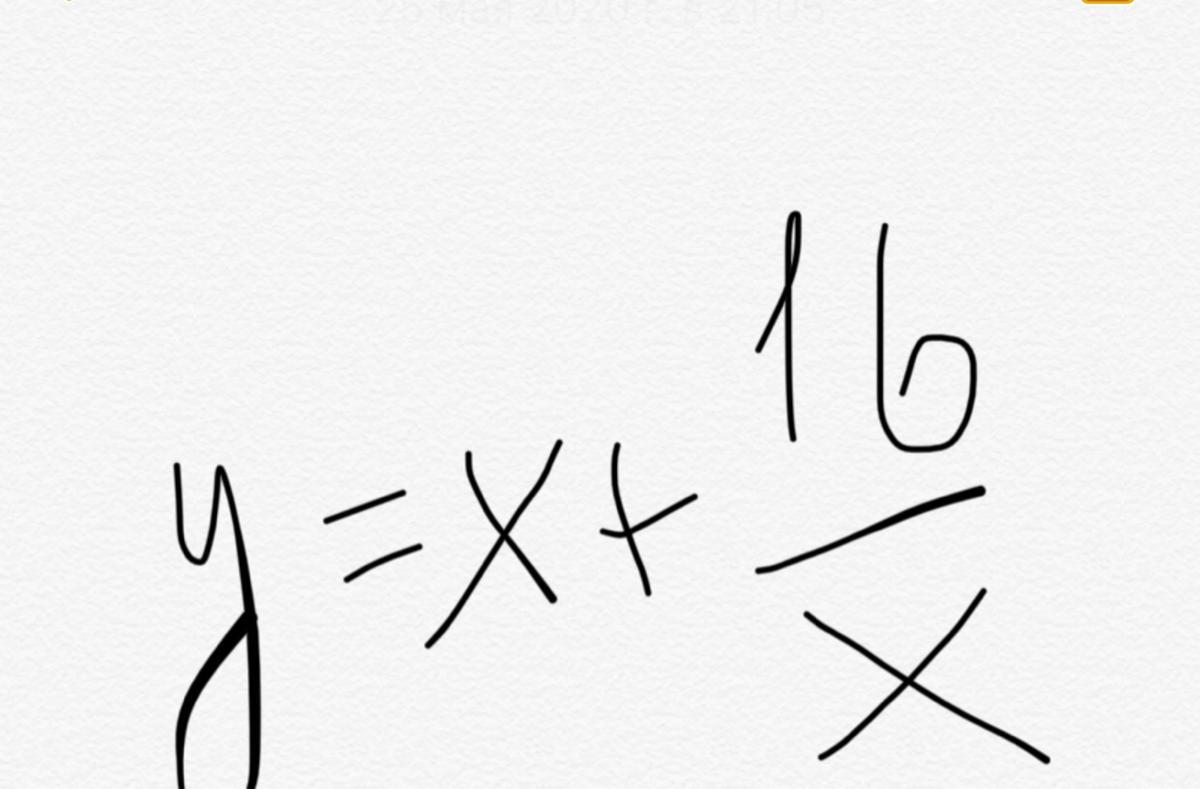
Ответы
Автор ответа:
8
Ответ:
(см. объяснение)
Объяснение:
y'=(x+16/x)'=1+(16x^(-1))'=1-16x^(-2)=1-16/x²
1-16/x²=0
x=+-4
y'(-5)=1-16/25=9/25
y'(1)=1-16=-15
y'(5)=1-16/25=9/25
На промежутке [-4; 4] функция убывает, а на оставшихся промежутках возрастает.
Тогда наименьшее значение функции на отрезке [1/2; 8] при x=4:
y(4)=4+4=8 - наименьшее значение функции на отрезке [1/2; 8].
Наибольшее значение либо при x=1/2, либо при x=8:
y(8)=8+2=10
y(1/2)=1/2+32=32.5 - наибольшее значение функции на отрезке [1/2; 8].
Похожие вопросы
Предмет: Английский язык,
автор: Asterious
Предмет: Русский язык,
автор: fedyasobyanin
Предмет: Русский язык,
автор: PrivetMir
Предмет: Химия,
автор: Аноним
Предмет: Алгебра,
автор: elenagolubeva1