Предмет: Геометрия,
автор: ForeignAgent
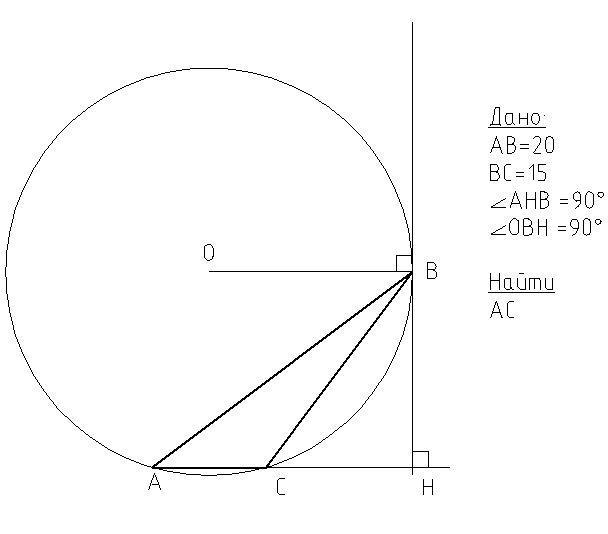
Дано:
Окружность с центром О, треугольник АВС вписанный в эту окружность, касательная к окружности ВН
АВ=20, ВС=15,
ВН перпендикулярна АС
Найти АС
За спам минус баллы и бан, как обычно.
Приложения:
Simba2017:
ответ 7 вышел
но долго, да и пишут уже
правильно 7
там теорема о касательной и секущей и пифагора
я составила систему 3 уравнений с 3 неизвестными
Пока на публикуй, новичкам хочу баллы дать
да пишет не новичок))))))))
да вижу уже ))
новички угроз испугались
вот и молодцы
Ответы
Автор ответа:
1
Ответ: AC=7 .
Объяснение:
Обозначим α=∠ВАС , он опирается на дугу ВС, значит равен половине угловой величины дуги ВС.
Угол между касательной ВН и хордой ВС равен половине угловой величины дуги, заключенной между ними.,то есть дуги ВС .
Значит, ∠ВАС=∠СВН .
Отрезок ВН равен радиусу окружности: r=BH .
Из ΔАВН: .
Из ΔВСН: .
Из ΔАВН:
Из ΔВСН:
вы не писали, что вам надо несколько способов...
нет-нет все нормально. еще раз спасибо Вам. мне не надо, у меня спортивный интерес ))
я же не знала, что это для учеников тренировка...думала, что какому-то ученику надо...
не верьте ему, он сам не решил
тогда всё это странно...
если бы не решил тебе не сказал бы что ответ 7
в ответ мог посмотреть
это не из сборников задача. иди помоги кому-нить лучше.
сам иди и помоги
будем теперь знать, что ваши задачи решать не стоит ради вашего спортивного интереса....
Похожие вопросы
Предмет: Английский язык,
автор: elyagontova
Предмет: Русский язык,
автор: timoshkov98
Предмет: Английский язык,
автор: kabargin
Предмет: Математика,
автор: коректор342