Предмет: Геометрия, автор: evaasp

7 класс, 80 баллов!
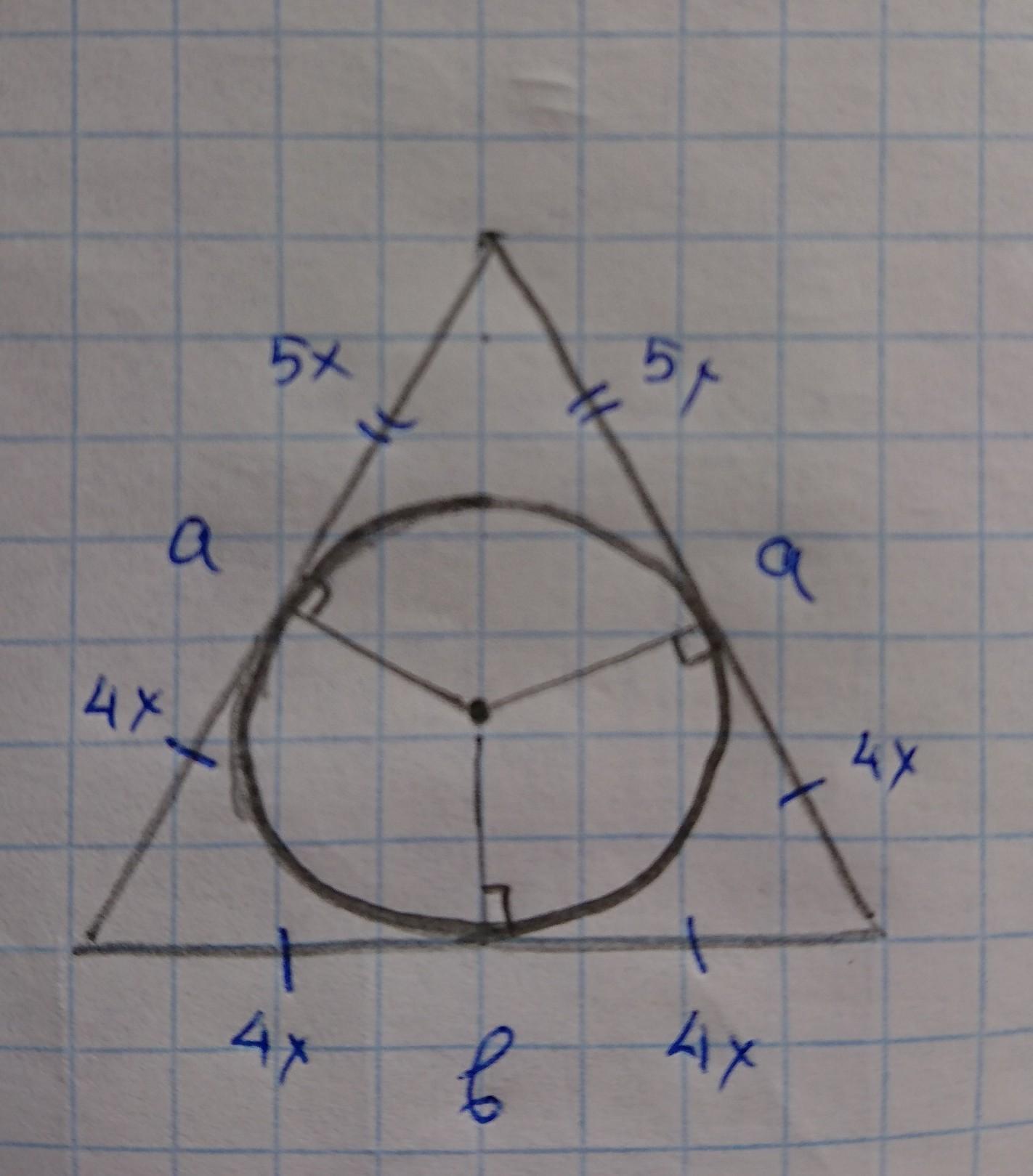
Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 4 : 5, считая от вершины угла при основании треугольника. Найдите стороны треугольника, если его периметр равен 104 см.

Ответы

Автор ответа: UncleGreg

Ответ:

Боковые стороны: a = 36 см

Основание: b = 32 см

Объяснение:

Пусть боковая сторона

a = 5x + 4x = 9x

Для вписанной фигуры отрезки касательных от пересечения касательных до т. касания равны. Нам известно, что такой отрезок боковой стороны от основания до т. касания = 4x. Тогда длина основания b = 4x + 4x = 8x

Периметр равнобедренного треугольника

P = 2*a + b = 2*(5x + 4x) + (4x + 4x) = 2*9x + 8x = 26x = 104 см

x = 4 см

Боковые стороны: a = 5x + 4x = 9*4 = 36 см

Основание: b = 4x + 4x = 8*4 = 32 см

Приложения:

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Русский язык, автор: лошадкаком

что значит для вас труд???

1 год назад

Предмет: Английский язык, автор: Аноним

помогите плиз ребят   Ticket 17

Прочитайте текст. Заполните пропуски 1-8 частями
предложений, обозначенные буквами A - I. Одна из частей лишняя.

A. After the last animal walked onto the ark, it
started to rain.

B. They caught
fish and enjoyed their voyage.

C. He was kind to all people.

D. They were safe with the animals on the ark.

E.   One day the bird returned with an olive branch in
his mouth.

E   Noah started to build the ark.

G. But Noah could not help them.

H. Most people on the earth are not as
kind as you.

I.
The sun appeared.

Noah's Ark

Noah was a very good man. He was not wealthy, but he was
honest and he worked hard. (1) He
believed in God and he prayed every day. He lived with his wife and
his children. One day, God spoke to Noah. He said, "Noah, I know that you
are a good man. (2) I am going to create a large storm.
I will destroy all of the bad things on the earth, but I will save
you and your family." Then God said,
"Build a large ark, Noah. Take your family on the ark with you. Also, take
two of every animal on the earth. Bring food and supplies for several months." (3) All of the people in the city
said that he was crazy, but Noah ignored them.
He believed what God said to him. Noah finished his ark. He
gathered his family and he gathered two of all of the animals on
the earth. (4) It rained and rained and rained. All of the people in
the city were frightened. They said, "Noah, help us! Let us
on your boat!" (5) It rained for forty days
and forty nights. It was the greatest flood ever. All of the people on the earth died in the flood. Noah and his
family floated on the water. (6) The rain stopped after forty days. (7)
"Noah wanted to see where land was. He
picked a bird from the ark. He said
to the bird, "I see only water around us. Fly away, bird! See if land is anywhere nearby!" But the bird
returned with no sign of land. Noah
continued this every day. (8) Noah saw the olive branch and understood that land was near. He said to his
wife, "Land is here! We are safe! God saved us!"

1 год назад

Предмет: Английский язык, автор: Bogryashooova

Помогите с заданием.перевидите предложения,раскройте скобки,поставьте глагол-сказуемое в нужную форму
образуйте отрицательную и вопросительную форму данных предложений.
the continuos (progressive) tenses
5. We (write) the difficult test now
6. She (sing) the beautiful song now
7. When he came home, his wife (prepare) the dinner
8. Next year we ( learn) English
9. We ( talk) over the telephone when the play ( begin)
10. She (sing) when we ( come)
the perfect tenses