Question

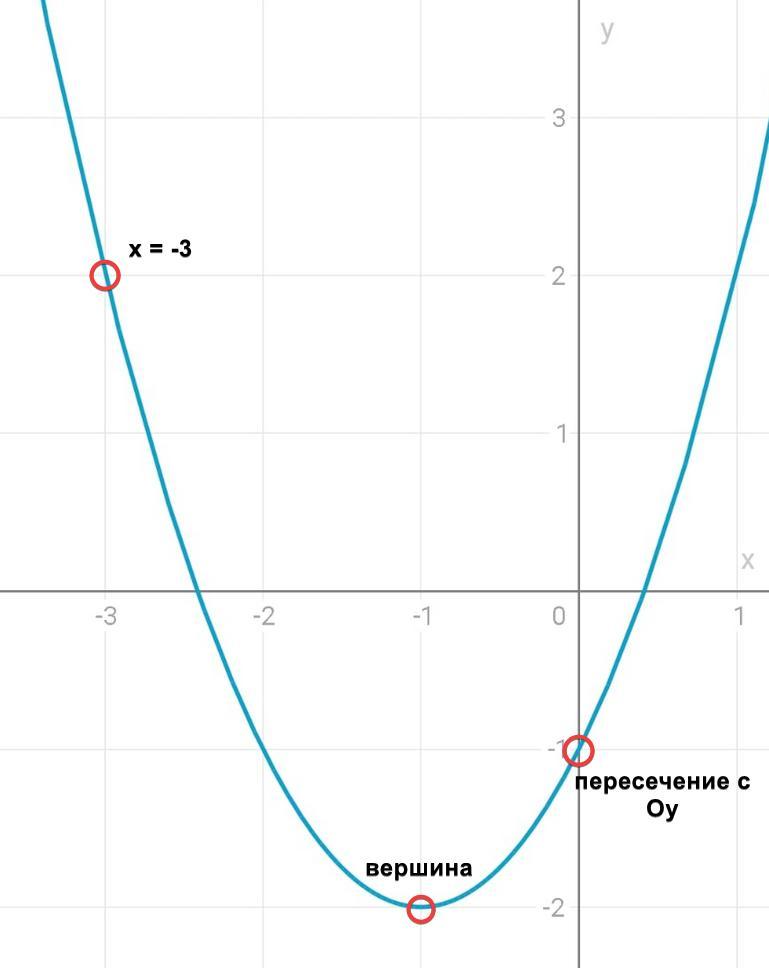
Построй график функции y=x2+2x−1.

Чтобы построить график, определи:
1) направление ветвей параболы (вниз или вверх)
;

2) точку пересечения графика с осью Oy (
;
);

3) координаты вершины параболы (
;
);

4) заполни таблицу значений:
x
−3
y

(Сравни построенный график с данным в шагах решений. Проверь, обозначены ли оси, отложен ли единичный отрезок, точен ли график).

Answer 1

Ответ:

$y=x^2+2x-1$

0) Это - квадратичная функция, график - парабола.

1) Так как коэффициент при $x^2$ положительный, ветви направлены вверх.

2) Пересечение графика с осью Oy: x = 0

$\left \{ {{x=0,} \atop {y=0^2+2*0-1;}} \right.\\\left \{ {{x=0,} \atop {y=-1.}} \right.$

Точка пересечения графика с осью Oy: (0;-1).

3) Вершина параболы:

$y_0=ax_0^2+bx_0+c, x_0=\frac{-b}{2a}\\x_0=\frac{-2}{2*1}=-1\\y_0=(-1)^2+2*(-1)-1=1-2-1=-2$

Вершина параболы: (-1; -2).

4)

$x = -3:\\y = (-3)^2+2*(-3)-1\\y=9-6-1\\y=3-1\\y=2$