Question

В правильной четырехугольной пирамиде все ребра равны 6. Найдите высоту пирамиды. А. 3 Б.3√2 В.9 Г.6√2

Answer 1

Ответ:

3√2

Пошаговое объяснение:

Все грани равны 6 см.

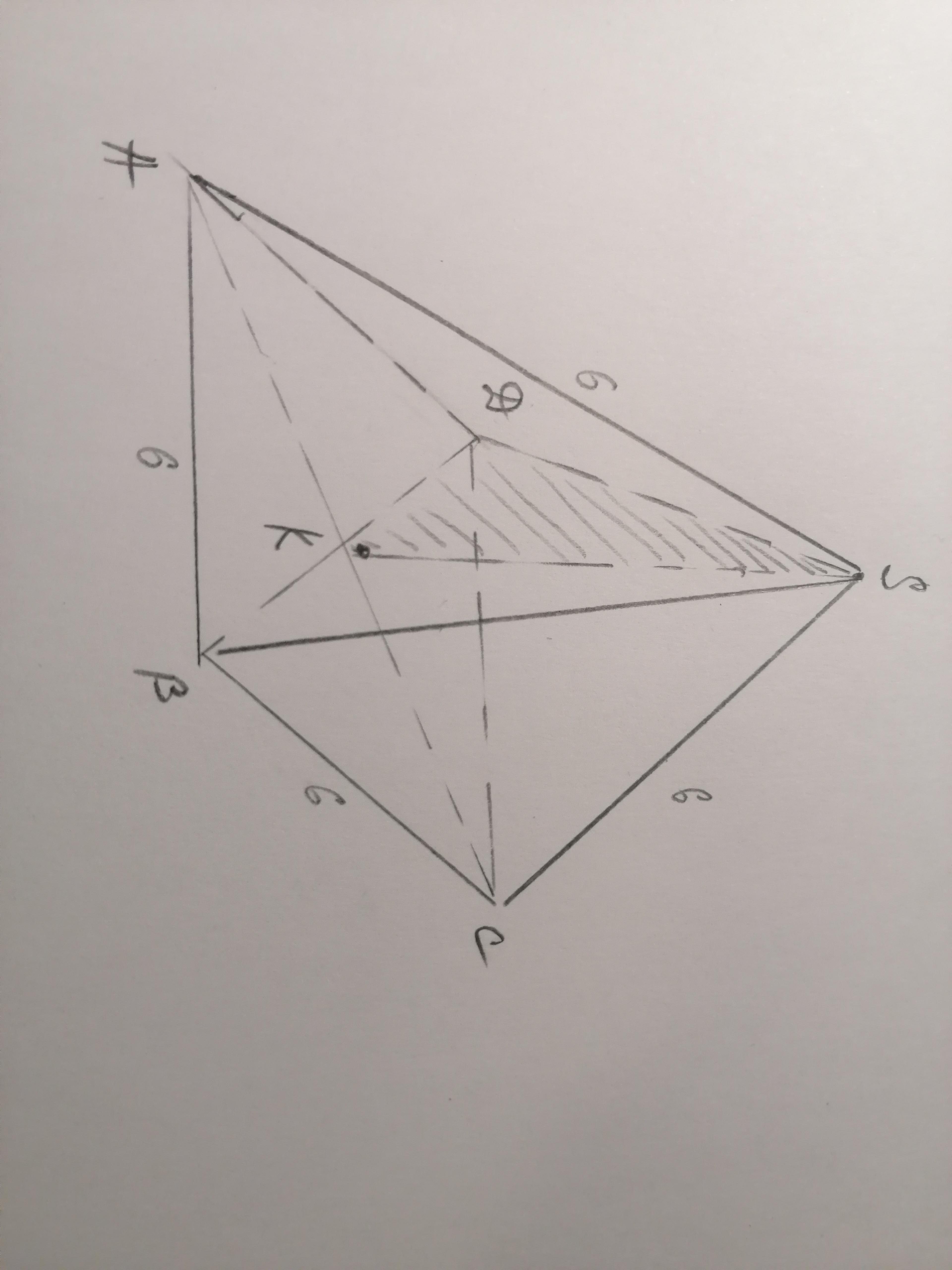
Найдем величину половины диагонали DВ (см вложенный рисунок)

Половина диагонали DВ⇒

Диагональ (DВ) по т Пифагора = √(6²+6²)=√72⇒половина диагонали (DК)=0,5√72

Теперь по той же теореме узнаем катет прямоугольного Δ КDS, который и является высотой правильной четырехугольной пирамиды:

h²=6²-(0,5√72)²=36-0,25*72=18⇒h=√18=√9*2=3√2