Предмет: Геометрия,
автор: dfmdbvpf
55 баллов.
7 класс.
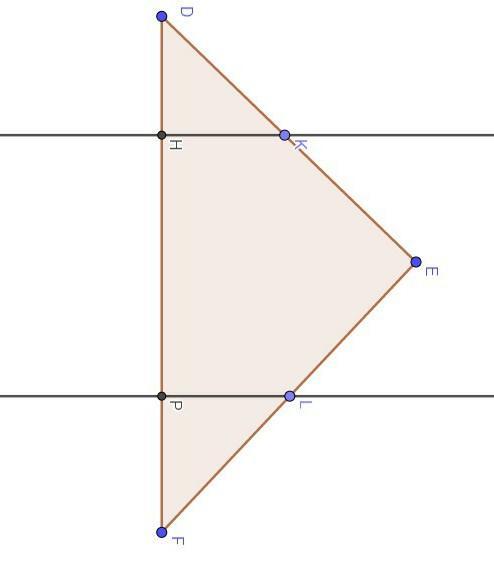
В треугольнике DEF на сторонах DE и EF отмечены точки K и L соответственно. Из этих точек опущены перпендикуляры KH и LP к прямой DF, причём KH=LP, ∠DKH=∠PLF. Докажите, что DE=EF.
Ответы
Автор ответа:
13
Если KH = LP, ∠DKH = ∠PLF, KH и LP - перпендикуляры, то △DKH = △FLP. Тогда ∠D = ∠F, а значит, △DEF - равнобедренный и DE = EF, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: oksanaperebeyn
Предмет: Русский язык,
автор: LOLbaby
Предмет: Английский язык,
автор: masha25list
Предмет: История,
автор: ксюша12001
Предмет: Математика,
автор: susanpipoyan1