Предмет: Алгебра,
автор: annamumm
Решите плиз! Тема новая, все сложно
Приложения:
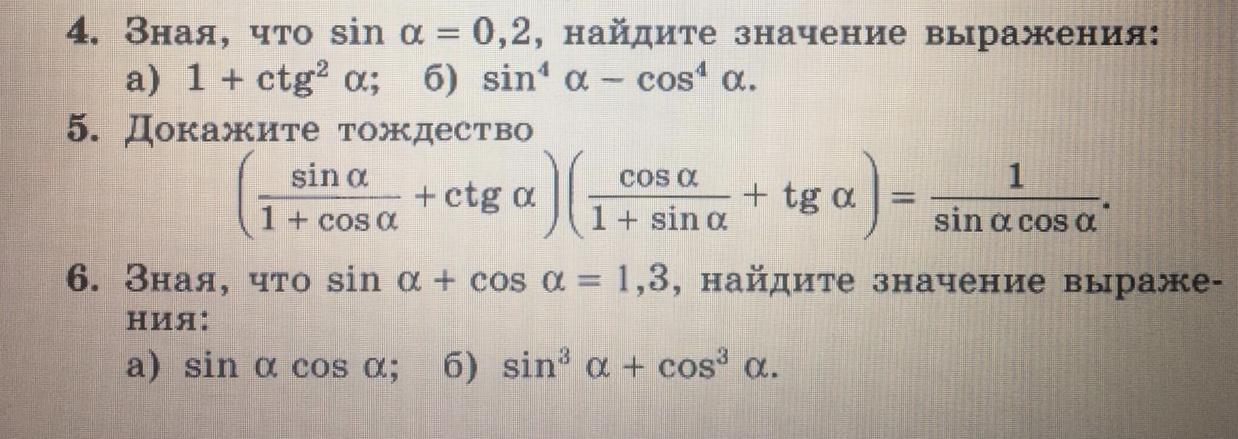
Ответы
Автор ответа:
1
Объяснение:
после каждой строки допишешь = 1/ sinācosā
Приложения:

annamumm:
Спасибо большое! За 4 сорян, не попала по 5 | (• ◡•)|
и на том спасибо :3
Автор ответа:
0
Ответ:
Объяснение:
4.
5.
6.
Похожие вопросы
Предмет: Українська література,
автор: nastasialova
Предмет: Русский язык,
автор: zigry
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: яна1544
Предмет: Химия,
автор: eva007dandelion