Предмет: Алгебра,
автор: erzan97
Помогите с этим примером
Приложения:
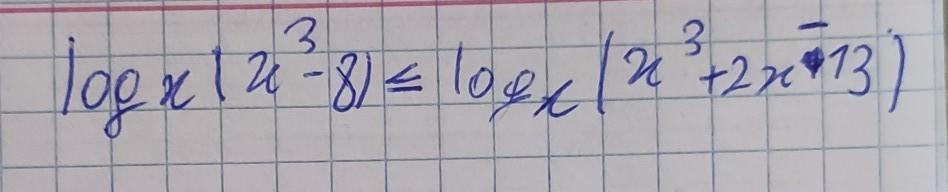
Ответы
Автор ответа:
3
logx(x³-8) <= logx(x³+2x-13)
logx(x³-8) - logx(x³+2x-13) <= 0
Метод рационализации:
{(x-1)(x³-8-(x³+2x-13)) <= 0
{x > 0, x ≠ 1
{x³-8 > 0
{x³+2x-13 > 0
1°)Сначала найду ОДЗ
{x > 0, x ≠ 1
{x³ > 8; x > 2
{x³+2x-13 > 0
f(x) = x³+2x-13
f'(x) = 3x²+ 2
f(x) возрастает на промежутке x > 0
f(2) = 8+6-13 = 14-13 = 1 > 0
Значит при x > 2 выполняется условие x³+2x-13 > 0
ОДЗ: x>2
2°)
(x-1)(x³-8-x³-2x+13) <= 0
(x-1)(-2x+5) <= 0
(x-1)(2x-5) >= 0
+. -. +
-------(1)--------[2.5]--------
x€(-∞; 1)U[2.5; + ∞)
Ответ: x€[2.5; +∞)
Похожие вопросы
Предмет: Русский язык,
автор: roshchupkinali
Предмет: Русский язык,
автор: Toralei2004
Предмет: Русский язык,
автор: 777866
Предмет: Алгебра,
автор: madness655
Предмет: История,
автор: shureckderugin402