Question

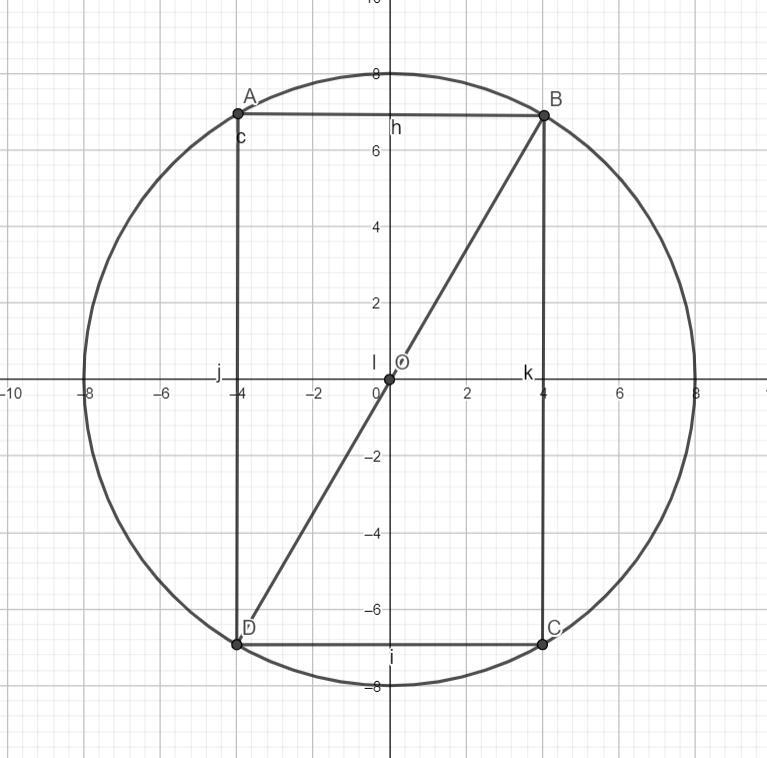
Четырёхугольник ABCD вписан в окружность радиуса 8 см, причём
стороны BC и AD параллельны и равны. Найдите AD, если ∠ABD = 60°.
Помогите срочно!!!

Answer 1

Ответ:

$4\sqrt{3}$

Объяснение:

вписанный четырехугольник будет прямоугольником (при равенстве оснований равностосторонняя трапеция превращается в  прямоугольник)

ΔADB - прямоугольный

DB - радиус окружности = 8 см

АB = 1/2 DB = 4 см - катет, противоположный углу 30 = половине гипотенузы

AD = $\sqrt{8^2-4^2}= \sqrt{48} = 4\sqrt{3}$