Предмет: Геометрия,
автор: Valera225mama
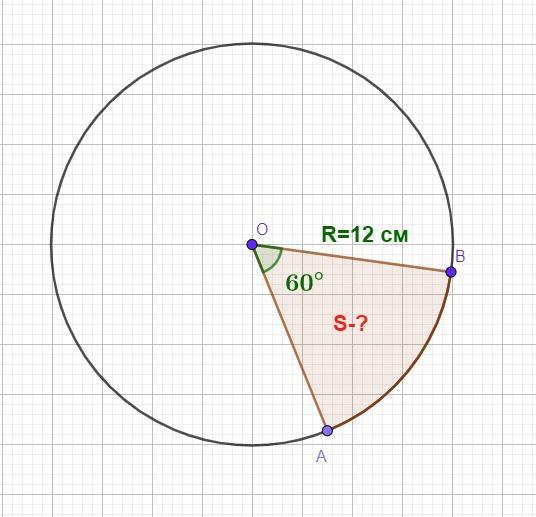
Знайдіть площу сектора круга радіуса 12 см, якщо відповідний йому центральний кут дорівнює 60 градусів
Ответы
Автор ответа:
1
Ответ:
Площа сектора круга радіуса 12 см дорівнює 24π см²
Объяснение:
Знайдіть площу сектора круга радіуса 12 см, якщо відповідний йому центральний кут дорівнює 60°
- Сектор круга - частина круга, обмежена дугою та двома радіусами, що з'єднують кінці дуги з центром круга.
Формула для обчислення площі кругового сектора:
де α - градусна міра відповідного центрального кута.
- Центральним кутом називають кут з вершиною у центрі кола.
За умовою: R = ОВ = ОА = 12 см, α = ∠АОВ = 60°, тоді:
см²
#SPJ5
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: terminator005
Предмет: Русский язык,
автор: шлргншлнг
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: Миша3111