Question

!!! ДАЮ СТО БАЛЛОВ !!! НЕ МОГУ РЕШИТЬ МЕСЯЦ УЖЕ

Answer 1

Ответ:

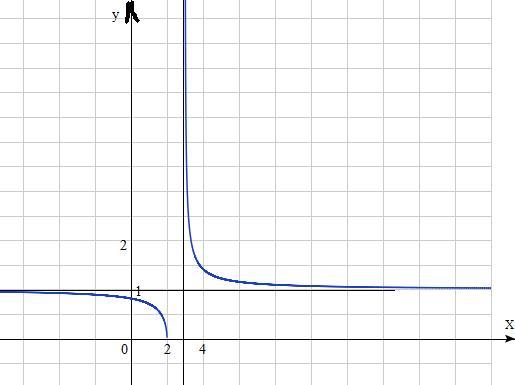
Построить график функции у=(√(х²-5х+6))/(х-3).Найти все значения а , при которых прямая у=а не имеет с графиком данной функции общих точек.

Объяснение:

Функция определена при  х-3≠0  и  х²-5х+6≥0.

Разложив на множители квадратный трехчлен   (х-3)(х-2)≥0 получим х≤2 и х≥3.   Учитывая х≠3 ⇒х≤2 , х>3.

Функция общего вида.

Преобразуем у=(√(х²-5х+6))/(х-3)

(√((х-3)(х-2))/(х-3)=(√(х-3)(х-2) )/√(х-3)²=√( (х-2)/(х-3))

у=√( (х-2)/(х-3))

у'=(√( (х-2)/(х-3)) )'=....... =0,5*√(х-3)(х-2)*(-5/(х-3) )

у'<0 при х-любом ,т.к -5<0, а х>3 ⇒ функция убывающая, точек экстремума нет.

х..-10........-8.......-2..........0.......1........2......4.......6

у..0.96..0.95....0.89...0.82..0,81...0...1.41....1.15.

Прямая у=а не имеет с графиком данной функции общих точек при а<0, а=1.

PS/

Lim√( (х-2)/(х-3))= Lim√( ((х-3)+1)/(х-3))= Lim√( 1+1/(х-3))=1 ,

х→∝                        х→∝                              х→∝

у=1  , горизонтальная асимптота