Предмет: Геометрия,
автор: z29112006z
От точки A к прямой проведены перпендикуляр AL и наклонная AM.
Определи расстояние от точки A до прямой, если сумма длин перпендикуляра и наклонной равна 11 см, а разность их длин — 1 см.
Ответ: расстояние от точки до прямой равно
см.
срочнооооооо))))) даю 43 баллов УМОЛЯЮЮЮЮЮЮЮ
Ответы
Автор ответа:
5
Ответ: AL=6
Объяснение:
AL+AM=11
Очевидно, что AL<AM, т.к. длинна перпендикуляра длинне наклонной (ну хотя-бы по тому, что в прямоугольном треугольнике ALM, AM - гипотенуза, а AL- катет)
AM-AL=1
AM=AL+1 - что и подставляем в первое равенство
AL+(AL+1)=11
2*AL=12
AL=6, а AL и есть расстояние до прямой
Lizzie2018:
Неверно. Вы не правильно уравнение решили
Автор ответа:
8
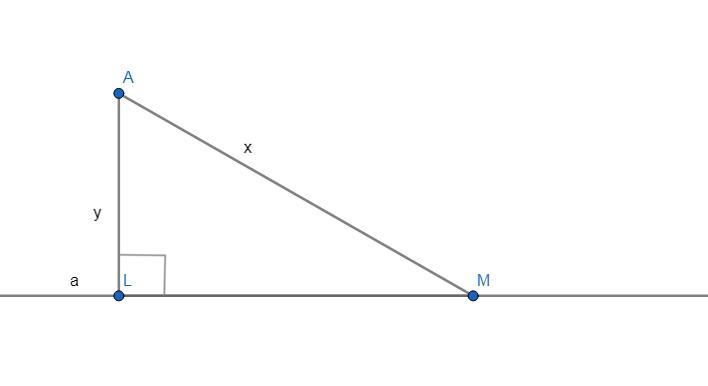
Чертёж смотрите во вложении.
Дано:
а - прямая.
АL - перпендикуляр от точки А до прямой а.
АМ - наклонная от точки А до прямой а.
∠ALM = 90°.
АМ+AL = 11 см.
Разность длин наклонной и перпендикуляра = 1 см.
Найти:
Расстояние от точки А до прямой а = ?
Решение:
- О каком расстоянии идёт речь в задании? Дело в том, что расстояние от точки до прямой - длина перпендикуляра, проведённого из этой точки к этой прямой. Поэтому, мы будем искать длину перпендикуляра AL.
- Так как АМ - наклонная, то она больше перпендикуляра AL (это не сложно доказать, если рассмотреть получившиеся прямоугольный ΔALM). Итак, поэтому, AM-AL = 1 см.
- Введём переменные. Пусть АМ = х, а AL = y.
- Составим систему линейных уравнений и решим её методом подстановки -
- AL = y = 5 см.
Ответ: 5 см.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: scorpion2014
Предмет: Русский язык,
автор: хфолод
Предмет: Українська мова,
автор: semenuk200
Предмет: Математика,
автор: annakiseleva02
Предмет: Математика,
автор: zhilec422