Question

К окружности с центром 0 проведите касательную CD ( D - точка касания ) найти радиус окружности если CO=22 см и угол COD=60°

Answer 1

Решение:

Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

=> OD ⊥ CD.

=> ∆COD - прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90°.

=> ∠OCD = 90° - 60° = 30°

Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.

Напротив лежащий катет OD - и есть радиус.

=> OD = 22 ÷ 2 = 11 см.

Ответ: 11 см.

Answer 2

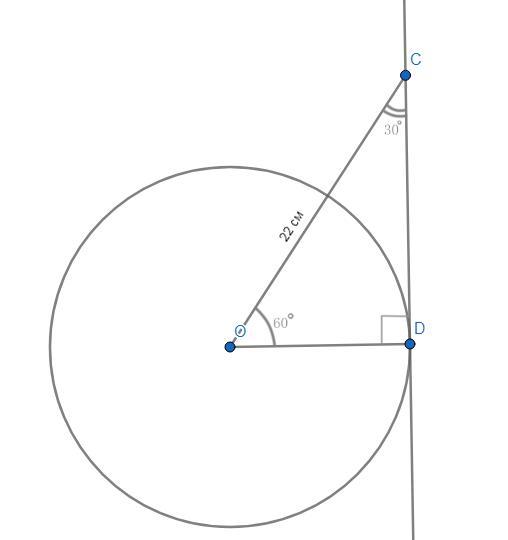
Чертёж смотрите во вложении.

Дано:

Окружность с центром О.

CD - касательная.

D - точка касания.

OD - радиус.

ОС = 22 см.

∠COD = 60°.

Найти:

ОD = ?

Решение:

• Радиус, проведённый в точку касания перпендикулярен этой касательной. Следовательно, ΔCOD - прямоугольный.
• Рассмотрим ΔСOD - прямоугольный. ∠OCD = 90°-∠COD = 90°-60° = 30° (так как сумма острых углов прямоугольного треугольника равна 90°).

• Против угла в 30° лежит катет, равный половине гипотенузы. В нашем случае гипотенуза - СО, так как лежит против угла в 90°. OD - тот самый катет, лежащий против угла в 30°. Поэтому, OD = 0,5*СО = 0,5*22 см = 11 см.

Ответ: 11 см.