Question

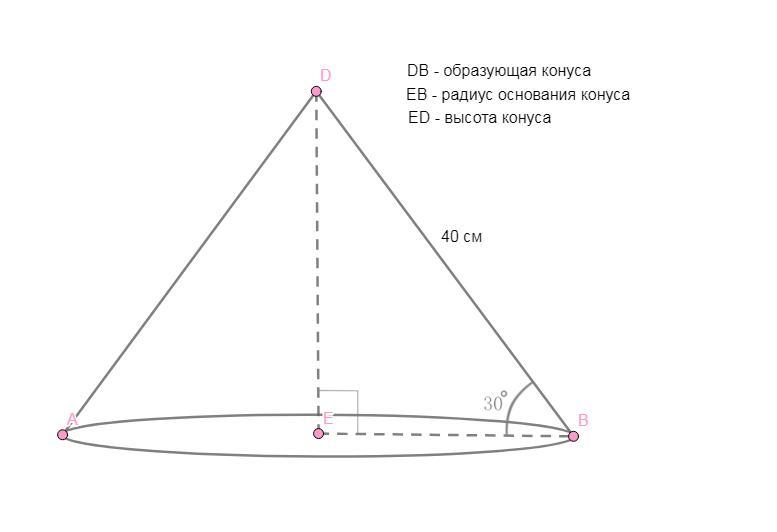
Образующая конуса 40 см наклонена к плоскости основания под углом 30°. Найдите высоту конуса, радиус основания, площадь полной поверхности конуса.
Помогите пожалуйста Рисунок и решение.
Заранее спасибо

Answer 1

Рассмотрим ΔDEB прямоугольный.

∠DBE = 30°.

Против угла в 30 градусов лежит катет, равный половине гипотенузы. Следовательно, ED = 40 см:2 = 20 см.

cos(∠DBE) = EB/DB

√3/2 = EB/40 см

ЕВ =20√3 см.

S (полной поверхности) = πr(r+ l)

Где r - радиус основания, l - образующая конуса.

S (полной поверхности) = π*20√3*(20√3+40) = π*20√3*20*(√3+2) = π*400√3*(√3+2) см².