Question

Срочно !!!
Зовнішній кут при основі рівнобедреного трикутника у 4 рази більший за суміжний з ним внутрішній кут. Знайдіть кути рівнобедреного трикутника.

Answer 1

Дано:

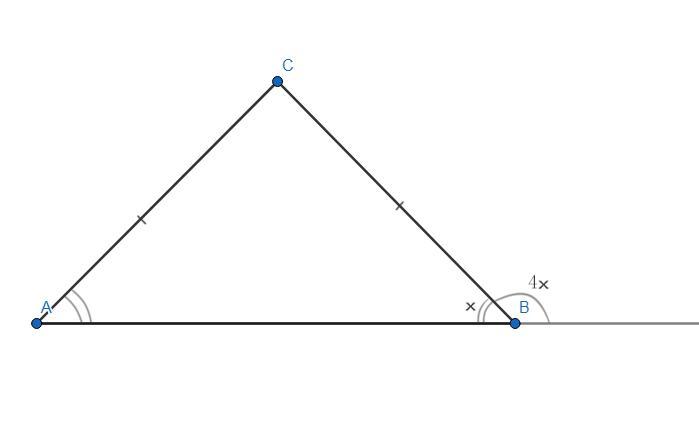
ΔАВС - равнобедренный (АВ - основание).

Внешний ∠В > ∠АВС в 4 раза.

Найти:

∠САВ = ?

∠АВС = ?

∠АСВ = ?

Решение:

Пусть ∠АВС = х, тогда внешний ∠В = 4х.

Так как ∠АВС и внешний ∠В - смежные, то их сумма равна 180°.

Составим линейное уравнение -

4х+х = 180°

5х = 180°

х = 36°

∠АВС = х = 36°.

Но так как ΔАВС - равнобедренный, то углы у основания ∠АВС= ∠САВ = 36° (по свойству равнобедренного треугольника).

Тогда, по теореме о сумме углов треугольника -

∠АСВ = 180°-∠АСВ-∠САВ = 180°-36°-36° = 108°.

Ответ: 36°, 36°, 108°.

Answer 2

Ответ:

36,36,108

Объяснение:

Нехай х-кут А тоді 4х-зовнішній кут кута А. сума суміжних кутів 180 градусів.

4х+х=180

5х=180

х=36

Отже, кут А= куту С = 36 градусів.

кут В =180-36-36 = 108 градусів

В-дь: 36градусів, 36 градусів, 108 градусів