Question

Срочно! Многочленів балов
Знайдіть площу трапеції, основи якої дорівнюють 16 см і 30 см, а бічні сторони - 13 см і 15 см

Answer 1

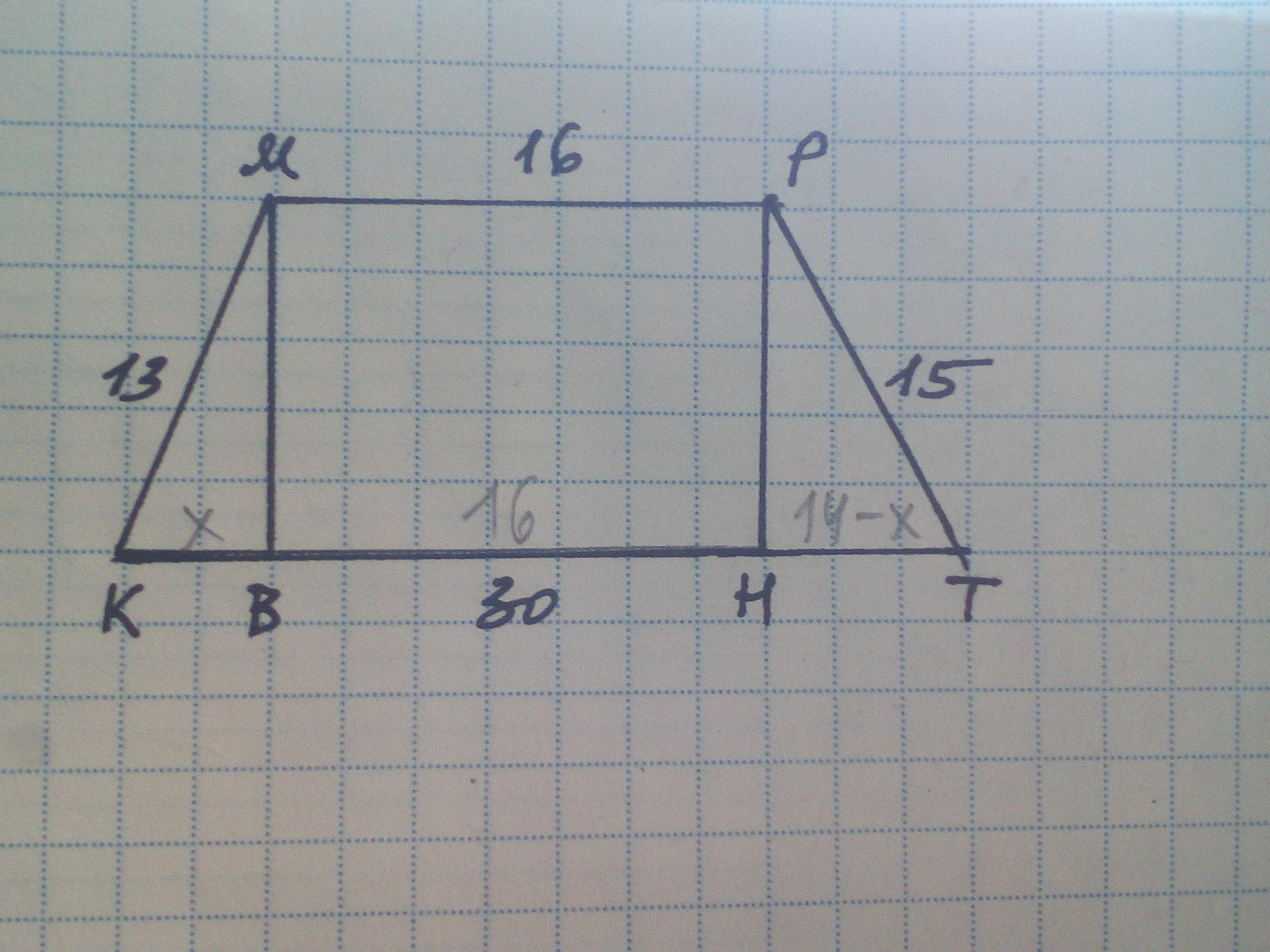
Дано: КМРТ - трапеція, МР=16 см, КТ=30 см, МК=13 см, РТ=15 см. Знайти S(КМРТ).

Площа трапеції дорівнює напівсумі основ помноженій на висоту.

Проведемо висоти МВ та РН.

ВН=МР=16  см,  КВ+ТН=30-16=14 см.

Нехай КВ=х см, тоді ТН=14-х см.

Розглянемо ΔКМВ та ΔТРН - прямокутні.

За теоремою Піфагора МВ²=МК²-КВ²  та РН²=РТ²-ТН².

Оскільки МВ=РН, маємо:

13²-х²=15²-(14-х)²

169-х²=225-196+28х-х²

28х=140;  х=5.

КВ=5 см, отже за теоремою Піфагора

МВ=√(МК²-КВ²)=√(169-25)=√144=12 см.

S=(МР+КТ):2*МВ=(16+30):2*12=276 см²

Відповідь: 276 см²