Question

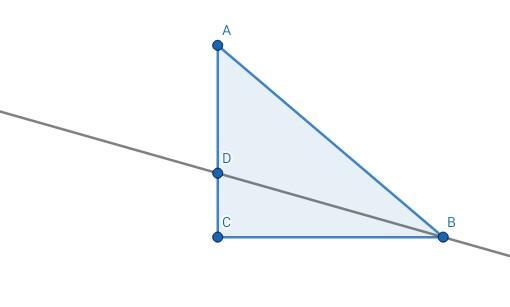
1) В треугольнике ABC угол C равен 90°, ВД - биссектриса, угол АДВ равен 110°. Найдите угол ВАД.
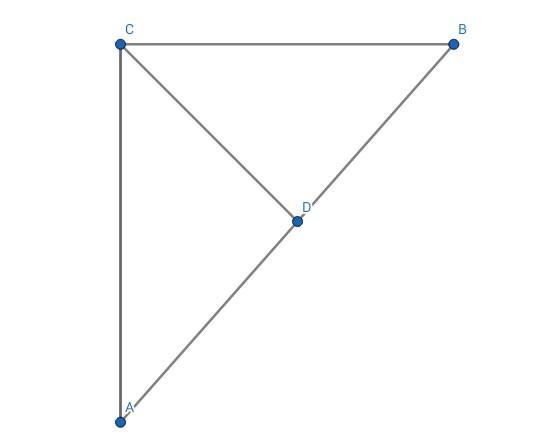
2)В треугольнике ABC угол С равен 90°, СД - высота, равная 8 см,
угол В равен 45 градусов. Найдите AB.​

Answer 1

Решение:

Задача#1.

Сумма смежных углов равна 180°.

∠ADB смежный с ∠BDC => ∠BDC = 180° - 110° = 70°

Сумма углов треугольника равна 180°.

=> ∠DBC = 180° - (90° + 70°) = 20°

Так как BD - биссектриса => ∠DBC = ∠DBA = 20°

∠DBC = ∠DBA = 20°=> ∠ABC = 20 × 2 = 40°

Сумма углов треугольника равна 180°.

=> ∠BAD = 180° - (90° + 40°) = 50°

Ответ: 50°.

Задача#2.

Сумма острых углов прямоугольного треугольника равна 90°.

=> ∠А = 90° - 45° = 45°

Так как ∠А = ∠В = 45° => ∆АВС - равнобедренный.

=> CD - высота, медиана, биссектриса.

Медиана, проведённая из прямого угла к гипотенузе, равна половине гипотенузы.

=> АВ = 8 × 2 = 16 см.

Ответ: 16 см