Предмет: Геометрия,
автор: st310705
Сочно!!! Помогите пожалуйста!
В равнобокую трапецию вписали окруж 43 ность. Из вершины одного её тупого угла
на основание опустили высоту. Докажите,
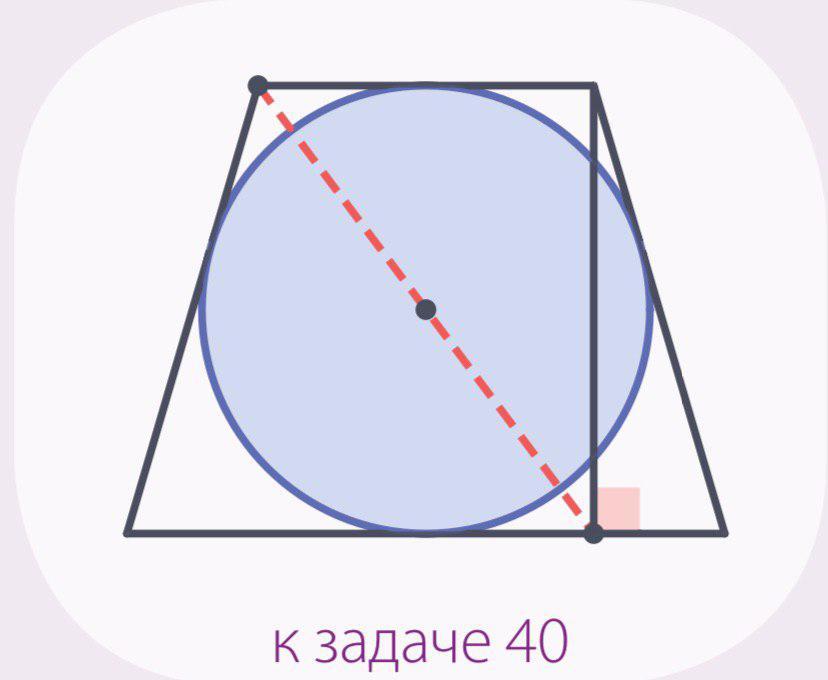
что отрезок, соединяющий основание этой высоты с вершиной другого тупого угла трапеции, проходит через центр данной окружности.
Приложения:
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Проведем через середину малого основания перпендикуляр а до пересечения с гипотенузой большого прямоугольного тр-ка в т.О
Отсекаемый от него малый прямоуголный тр-к будет ему подобен по 2-м углам (90 и один общий). Значит и их элементы подобны. Коэф. подобия k=1/2 (т.к. через середину основания провели и их катеты имеют такое отношение). Тогда a/h = 1/2, а это может быть только в том случае, если r/D =1/2, т.е. D=2r, следовательно точка О - это центр окружности. ч.т.д.
Похожие вопросы
Предмет: Другие предметы,
автор: suti
Предмет: Другие предметы,
автор: Карина0Князева
Предмет: Українська мова,
автор: Lazareva1966
Предмет: Математика,
автор: G0dz1la
Предмет: Математика,
автор: Rivela