помогите пожалуйста с решением работы по алгебре
11 класс
много баллов!
1) найти dz/dx и dz/dy , если z=y^xy
2) найти dz/dx и dz/dy , если z=sin u^5/v^3 , где u= корень x-y , v=e^2x
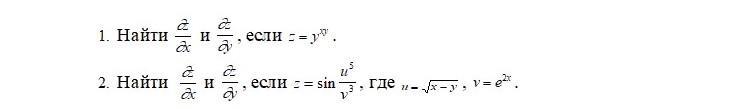
Ответы
Ответ:
Объяснение:
1) z = y^(xy)
dz/dx = y^(xy)*ln |y|*y
dz/dy = (xy)*y^(xy-1) + y^(xy)*ln |y|*x = y^(xy)*(xy*1/y + x*ln |y|) =
= y^(xy)*x*(1 + ln |y|)
2) z = sin(u^5)/v^3; u = √(x-y); v = e^(2x)
Сначала напишем промежуточные дифференциалы:
dz/du = 1/v^3*cos(u^5)*5u^4 = 5u^4/v^3*cos(u^5)
dz/dv = sin(u^5)*(-3)*v^(-4) = -3/v^4*sin(u^5)
du/dx = 1/(2√(x-y))
du/dy = -1/(2√(x-y))
dv/dx = 2e^(2x)
dv/dy = 0
Теперь пишем главные дифференциалы:
dz/dx = (dz/du)*(du/dx) + (dz/dv)*(dv/dx) =
= 5u^4/v^3*cos(u^5)*1/(2√(x-y)) - 3/v^4*sin(u^5)*2e^(2x) =
= 2,5u^4/v^3*cos(u^5)*1/√(x-y) - 6/v^4*sin(u^5)*e^(2x)
dz/dy = (dz/du)*(du/dy) + (dz/dv)*(dv/dy) =
= 5u^4/v^3*cos(u^5)*[-1/(2√(x-y))] - 3/v^4*sin(u^5)*0 =
= -2,5u^4/v^3*cos(u^5)*1/√(x-y)
Ответ:
Следует отметить, что когда вычисляется частная производная от функции многих переменных по некоторой переменной, то остальные переменные рассматриваются как константы.
1) Дана сложная функция двух переменных
Находим частные производные.
Так как переменная х участвует только в показателе функции z(x, y), то частную производную по х находим как от показательной функции с основанием y, в показателе которой сложная функция:
Ответ:
Для нахождения частную производную по у поступим следующим образом.
а) Логарифмируем по основанию e обе стороны выражения :
б) Находим частную производную по у от левой части последнего выражения:
Находим частную производную по у от правой части последнего выражения как производная от произведения:
в) Имеем:
или
Ответ:
2) Дана сложная функция двух переменных
Находим частные производные как от сложной функции.
Частная производная по х:
Ответ:
Частная производная по у:
Ответ: