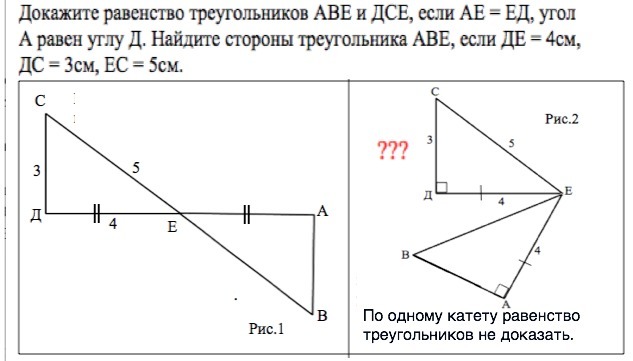
13. Докажите равенство треугольников АВЕ и ДСЕ, если АЕ = ЕД, угол А равен углу Д. Найдите стороны треугольника АВЕ, если ДЕ = 4см, ДС = 3см, ЕС = 5см.
Ответы
---------
а) Отношение сторон треугольника ДEC 3:4:5 - он "египетский", т.е. прямоугольный с катетами ДE и СД. Причём, т.к. катеты "встречаются" в т.Д, то угол EДC=90°.
Доказать равенство треугольников ABE и ДCE можно, если ВЕ и ЕС расположены на одной прямой, и АЕ и EД также расположены на одной прямой, т.е. ВС и АД пересекаются в т.Е.
Тогда:
В данных треугольниках равны два угла - данные по условию и вертикальные при Е, равны и стороны, к которым эти углы прилежат. -- треугольники АВЕ и ДСЕ равны по 2-му признаку равенства треугольников. (рис. 1 приложения)
б) Против равных углов в равных треугольниках лежат равные стороны ⇒
АВ=СД=3 см
AЕ=ЕД=4 см, BE=CE=5 см
---------
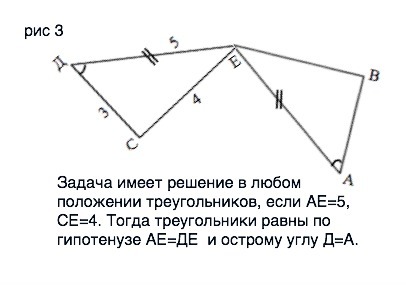
Рис. 2 - данных недостаточно. Рис. 3 - решение возможно при любом положении треугольников с общей вершиной Е.