Предмет: Геометрия,
автор: iluacher1071
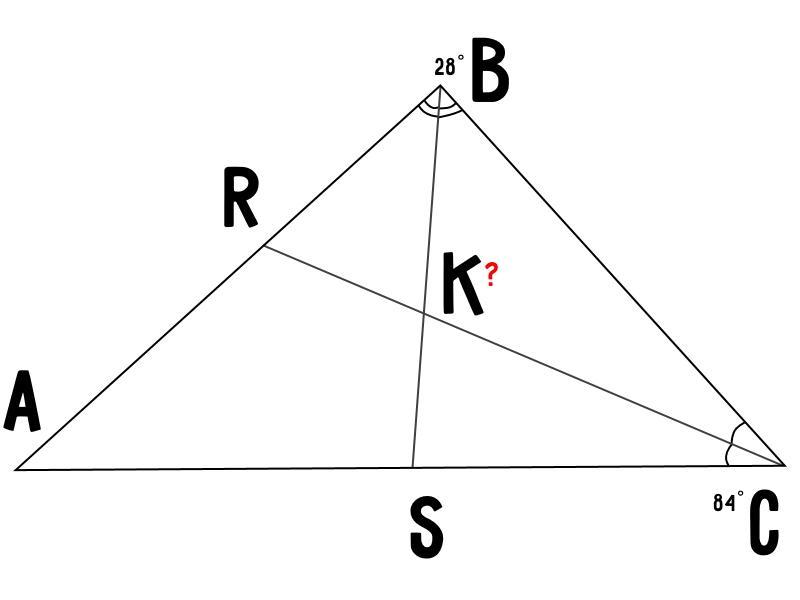
Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите < ВКС, если < В = 28˚, а < С = 84 ˚.
Ответы
Автор ответа:
1
Тогда с теоремы о сумме углов треугольника:
∠A + ∠B + ∠C = 180˚ ⇒
∠A = 180˚ - ∠B - ∠C = 180˚ - 28˚ - 84˚ = 68˚.
Так, как BS и CR - биссектрисы, то они делят:
∠B и ∠C пополам, из этого:
∠SBC = =
∠RCB = =
Тогда, с теоремы, о сумме углов треугольника:
∠SBC + ∠RCB + ∠ВКС = 180˚ ⇒
∠ВКС = 180˚ - ∠SBC - ∠RCB = 180˚ - 14˚ - 42˚ = 124˚.
Ответ: 124˚.
Рисунок:
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: dzhamalut
Предмет: Українська мова,
автор: РейнбоуДешРадугаДеш
Предмет: Русский язык,
автор: 11081999
Предмет: Алгебра,
автор: MissBagura