Question

Срочно !!!!!
1. Объем конуса равен 168. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
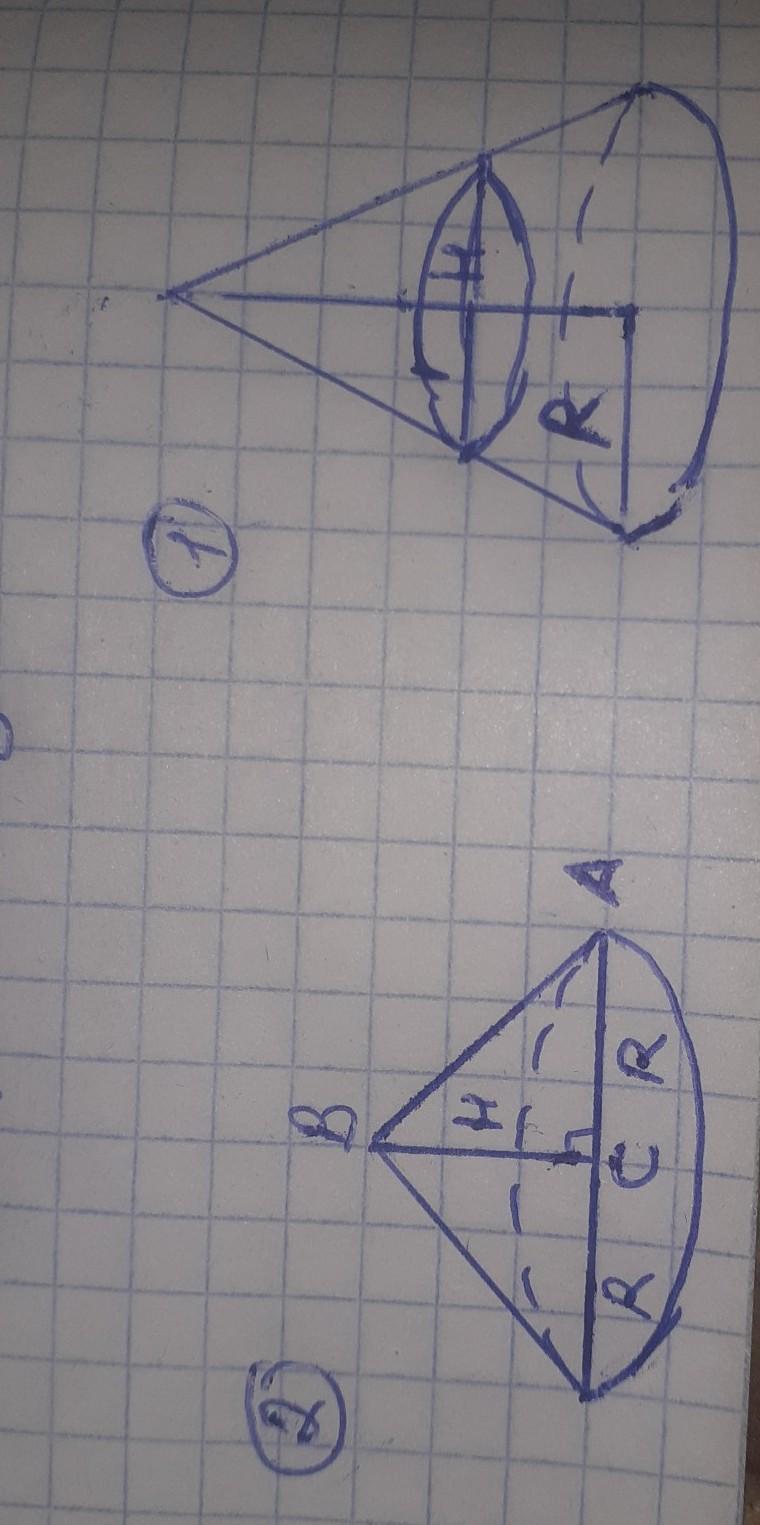
2. Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 30. Найдите его объем, деленный на .
3. Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 4. Найдите его объем, деленный на .
4. В треугольнике ABC угол C равен , . Найдите .
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Answer 1

1)

V=168

высота меньшего конуса

h1=H/2

радиус

r=R/2

V=1/3 × πR²H=168

объем меньшего конуса

Vм= 1/3 ×π×(R/2)²× H/2= 1/4×1/2× ( 1/3×πR²H)=1/8×V

Vм=168/8=21

2) Δ ABC прямоугольный равнобедренный треугольник

а=b=AC=BC=30

R=AC=30

H=BC=30

V=1/3 × πR²×H=1/3× π×30²×30=9000 π

3)

H=4

a=3

V - ?

конус описан около правильной четырёх угольной пирамиды, со стороной основания а=3.

диагональ d основания пирамиды равна диаметру D конуса.

d=a√2=3√2

D=d=3√2

радиус конуса R=D/2=3√2 /2

объем конуса

V=1/3 × πR²×H=1/3× π×( 3√2/2)² ×4= 6π