Верно ли утверждение?
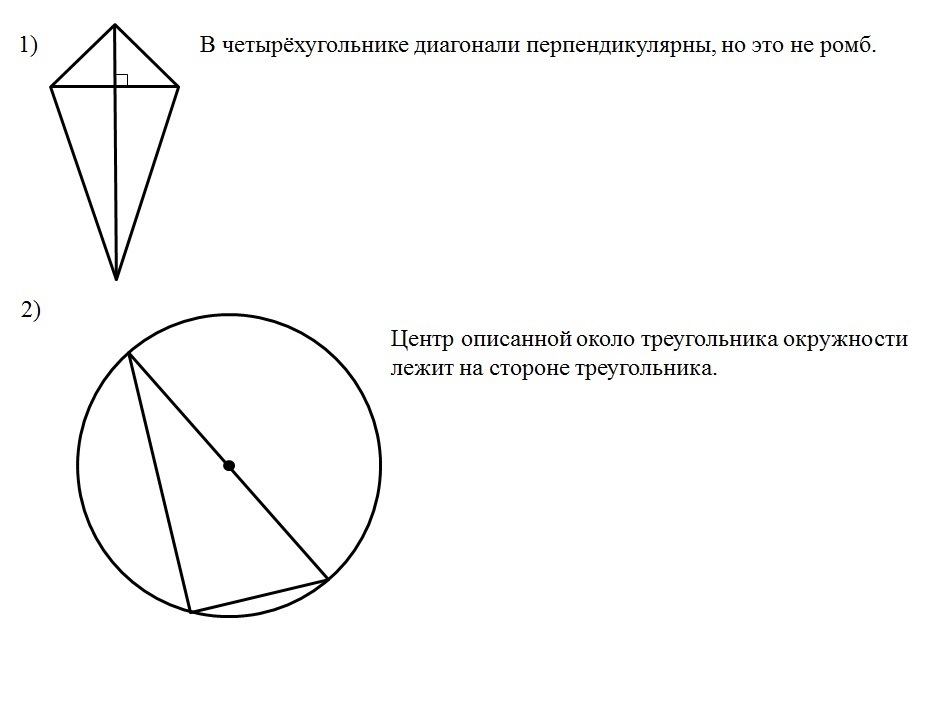
1) Если диагонали четырехугольника перпендикулярны, то этот четырехугольник - ромб.
2) Центр окружности, описанной вокруг треугольника, не может лежать на его стороне.
3) Треугольник со сторонами корень а, корень b и корень а+b - всегда прямоугольный.
4) Существует треугольник, в котором любая из высот меньше любой из медиан.
Ответы
1) Неверно. Это может быть дельтоид. Ещё может быть трапеция с перпендикулярными диагоналями. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб, но в условии дан произвольный четырёхугольник, а не параллелограмм.
2) Неверно. Центр описанной около прямоугольного треугольника лежит на гипотенузе. Так что центр описанной около треугольника окружности может лежать на стороне треугольника.
3) Верно.
Дан треугольник со сторонами: √a, √b, √(a + b).
Проверим по теореме, обратной к теореме Пифагора.
Если квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник прямоугольный:
(√(a + b))² = (√a)² + (√b)²
a + b = a + b. Верно.
Теорема обратная теореме Пифагора выполняется, следовательно, треугольник прямоугольный.
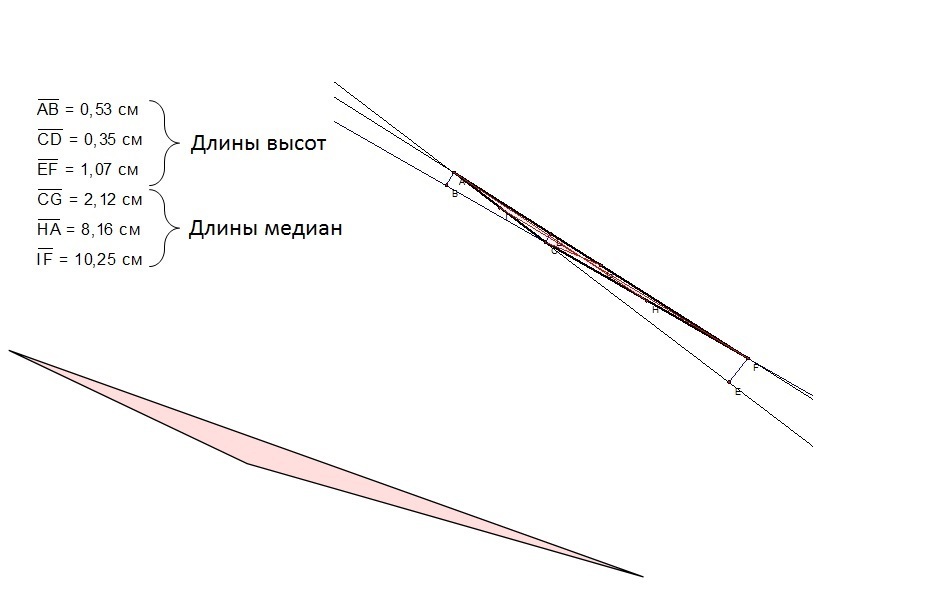
4) Верно. Существует треугольник, в котором любая из высот меньше любой из медиан?
Если хотя бы один такой треугольник привести в пример, то ответ на вопрос – да, существует. Приведу пример такого треугольника. Рассмотрим треугольник на приложенном изображении. Один из углов у него – тупой, причём, величина близка к 180°. Длины сторон – достаточно большие. Вот в таком треугольнике любая высота короче любой медианы. В приложении «Живая геометрия» измерены длины высот и медиан. Так что существование такого треугольника очевидно. Над геометрическим доказательством этого факта подумаю на досуге)))