Предмет: Алгебра,
автор: haicel
Разложение многочлена на множители способом группировки
Приложения:
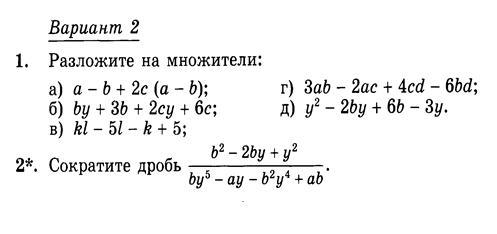
haicel:
только 2
Ответы
Автор ответа:
1
Ответ:
1.
а)а-b+2c*(a-b)=(a-b)*(1+2c)
б)by+3b+2cy+6c=b*(y+3)+2c*(y+3)=(y+3)*(b+2c)
в)kl-5l-k+5=l*(k-5)-(k-5)=(k-5)*(l-1)
г)3ab-2ac+4cd-6bd=a*(3b-2c)-2d*(3b-2c)=(3b-2c)*(a-2d)
д)
2.
.
Объяснение:
фух
Похожие вопросы
Предмет: Русский язык,
автор: 65катя
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: AlcoCat123
Предмет: Математика,
автор: Ванёк22811111
Предмет: Математика,
автор: Dregon109